ベクトル 円の方程式

ベクトル　円の方程式

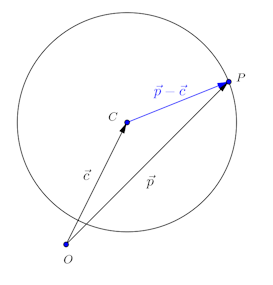
点を中心とする半径rの円のベクトルを用いた方程式は

　　

になる。ここでは円Cの円周上の点。

円の中心Cが原点の時は

　　

となる。

ベクトルの円の方程式の計算では内積の知識が必須なので、ベクトルの内積の復習。

ベクトルの内積は、ベクトルの大きさを、さらにのなす角度をθとすると

　　

である。

また、内積を

　　

とも表記する。

この定義から、

　　

であり、のとき

　　

である。

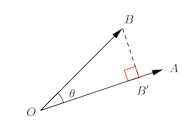
次に、内積の幾何学的な意味について考えることにする。

始点をOとするという２つのベクトルがあるとする。

BからOAにおろした垂線の足をB'とすると、

　　

よって、

　　

になる。

つまり、内積は、OAと、OBのOA上への正射影OB'との積と考えることができる。

ベクトルの内積については次のことが成り立つ。

　　

これを見るとわかるけれど、内積は実数同士の掛け算の自然な延長になっている。
だから、普通の実数同士の掛け算のように計算をしてよい。

これで準備は整った。

問題を解いてみることにする。

問題１　Oを原点とする平面上で、A、B、Cを定点、Pを動点とし、その位置ベクトルを

　　

とする。また、rを正の定数とするとき、次の条件を満たすPの軌跡は何か。

　　

【解】

（１）
　　

よって、

　　

となり、Pの軌跡はCを中心とする半径rの円周である。

（２）
　　

これは

　　

か

　　AP⊥BP

のいずれかで、

　　P=A、P=B、∠APB=90°

のどちらかであり、Pの軌跡はABを直径とする円周である。

（別解）

　　

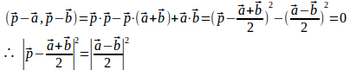
よって、Pの軌跡はABの中点を中心、AB/2を半径とする円周上である。

ここで、

　　

をあらわすものとする。

（解答終わり）

少し補足説明をすると、

∠APB=90°のとき、円周角の定理より、点PはABを直径とする円周上に存在することになる。そして、A=P、B=PからA、Bも含まれ、ABを直径とする円になる。

問題２　平面上で、A、Bは定点、Pは動点とする。また、cを正の定数とするとき、つぎの条件を満たす点Pの軌跡を求めよ。

　　

【解】

A、B、Pの位置ベクトルをとする。

（１）
　　

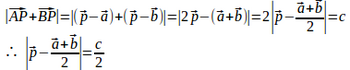
よって、ABの中点を中心とする半径c/2の円周。

（２）

　　

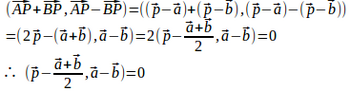
線分ABの中点をCとすると、

　　

はABの中点Cの位置ベクトルになり、

　　

これは、ABの中点Cと点Pを結ぶCPがABと直交しているということを意味しており、したがって、Pの軌跡はABの垂直二等分線である。

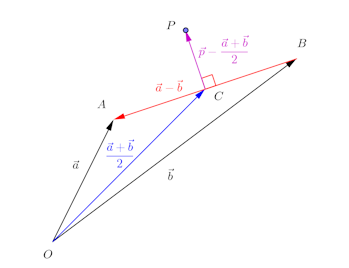
（別解）

　　

よって、Pの軌跡は線分ABの垂直二等分線としてもよい。

タグ：ベクトル