微分方程式の解法３

微分方程式の解法３

§１　定数係数の２階線形微分方程式の解法

高校の微分積分では、定数係数の２階微分方程式

　　

の解法を扱わない。

ではあるが、結論を先取りして言うならば、①の解は、２次方程式――特性方程式という――

　　

の相異なる実根をα、βとするとき、

　　

になる。

このことは知っておいて損はないだろう。

③が①の解になることは、

　　

とおくと、

　　

この結果を①に代入すると

　　

となり、αが２次方程式の解であることより

　　

したがって、これは微分方程式の①の解である。

同様に、も解であり、

このことから

　　

は①の解であることが証明できる。

また、逆に①がという形の解をもつとすれば、

　　

でなければならない。

粗い議論であるが、２次方程式①が相異なる②実根α、βをもつとき、微分方程式①の解が③になることを理解できるのではないか。

１階の微分方程式

　　

の一般解が

　　

であることは、

　　

として、④を解くことによって確かめられる。

そして、この場合も一次方程式

　　

を解くことによって、微分方程式の一般解を簡単に求められる。

しかし、この結果は高校の数学の範囲を超えているので、高校の微分積分ではこの解法を採用しないことにする。ではあるが、この議論は、微分方程式の解の確認に使えるので、知ったおいて損はないと思う。

問　次の微分方程式の解を求めよ。

【解】

（１）　特性方程式を解くと

　　

よって、一般解は

　　

（２）　特性方程式

　　

よって、一般解は

　　

（解答終了）

 

§２　連立微分方程式の解法

問題１　f'(x)=g(x)、g'(x)=f(x)、f(0)=1、g(0)=0を満たすような関数f(x)、g(x)を求めよ。

f(x)=y、g(x)=zとおくと、

　　

zを消去するために、①をxで微分すると

　　

yの一般解は問の（２）より

　　

この結果を①、②のどちらに代入してzを求めても良いが、積分の計算よりも微分の計算の楽なので①を使うことにする。

　　

①、②、ならびに、初期条件f(0)=1、g(0)=0より
　　

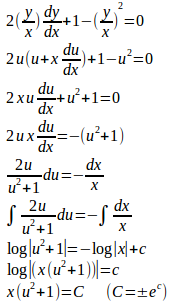
したがって、

　　

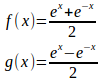
（解答終了）

このように解くことができるけれど、これは高校数学の範囲がの解法なので、この問題は次のように解くとよい。

【解】

　　

①＋②
　　

u=f(x)+g(x)とおくと

　　

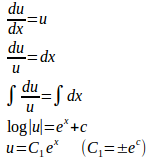
①−②

v=f(x)−g(x)とおくと

　　

よって、

　　

③と④、さらに、初期条件f(0)=1、g(0)=0より

　　

よって、

　　

⑤＋⑥
　　

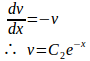
⑤−⑥

　　

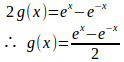
（解答終了）

問題２　平面上を運動するP(x,y)の両軸方向の速度について

　　

の関係があるとき、Pはどのような曲線上を動くか。

【解】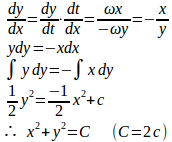
　　

（解答終了）

この連立微分方程式の解を求められないことはないのだけれど、これは高校の微分積分の範囲を大きく逸脱してしまうので、これ以上は解かないことにする。

タグ：微分積分