定積分と不等式2 [ネコ騙し数学]
定積分と不等式2
問題1 (シュワルツの不等式)
(1) a、bは定数で、a<bとし、f(x)とg(x)はa≦x≦bで連続な関数とする。a≦x≦bなる範囲で
(2) 次の不等式(シュワルツの不等式)を証明せよ。
(1)
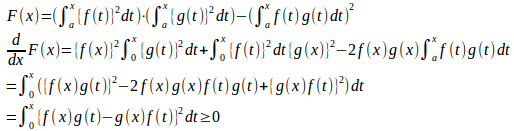
(2) (1)より、F'(x)はa≦x≦bでF'(x)≧0であり、また、F(a)=0。
よって、a≦x≦bでF(x)は増加関数で、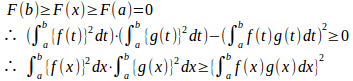
(解答終了)
シュワルツの不等式
の一般の証明法は次の通り。
a<b、そして、tを任意の実数とすると 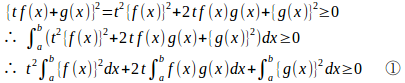
そして、問題1は、この別な証明である。
問題2 f(x)、g(x)をx≧0で定義された正の値をとる連続関数で、g(x)は連続関数であるとする。このとき、
(1) すべてのx>0に対してである。
(2) はx>0で増加関数である。
ここで一般に増加関数であるとは、x₁<x₂ならばh(x₁)≦h(x₂)が成立することをいう。
【解】(1) 仮定によって0≦t≦xにおいてg(0)≦g(t)≦g(x)。
また、f(t)>0だから
(2)
タグ:微分積分
ワンポイントゼミ22 定積分と不等式1の補足 [ネコ騙し数学]
ワンポイントゼミ22 定積分と不等式1の補足
定積分と不等式1で出てきた内容を補足することにする。
よって、
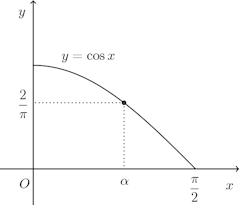 とする。
とする。
となり、x=0、x=π/2のときに最小で、最小値は0
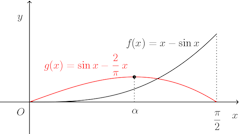 よって、0<x<π/2において
よって、0<x<π/2において
次に、
そこで、ロピタルの定理を使うと
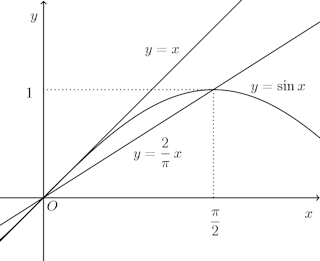
問題3の(1)のグラフで
x=0のところで白抜きの丸で表現されているのは、そういうわけです。
(下図参照)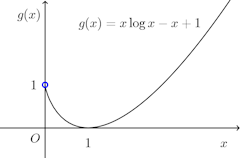
タグ:微分積分