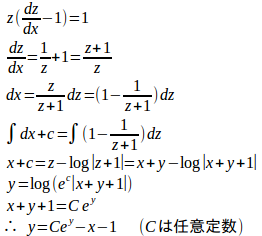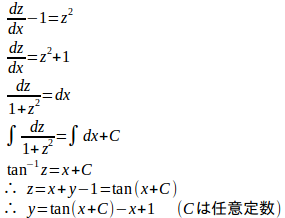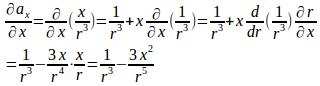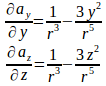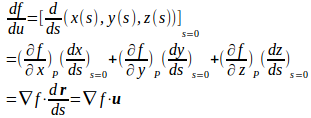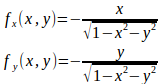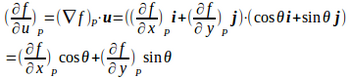第2回 変数分離法・問題編 [ネコ騙し数学]
第2回 変数分離法・問題編
問題1 次の微分方程式を解け。
【解】
(1)
(2)
(解答終)
問題2 次の微分方程式をカッコ内の置換をして解け。
【解】
(1) z=x+yの両辺をxで微分すると、
(2) z=x+y–1の両辺をxで微分すると、
よって、微分方程式は
(解答終)
問題3 x軸上を運動している点がある。速度について、加速度については
という関係があるものとする。f(0)=1のとき、f(x)を求めよ。
【解】
v=f(x)とおくと、
x=0のとき、f(0)=1だから、
(解答終)
問題3では、問われていないけれど、
だから、
第1回 変数分離形 [ネコ騙し数学]
第1回 変数分離形
未知関数yの導関数を含む方程式を微分方程式といい、これを満たす関数をその解、解を求めることを微分方程式を解くという。
微分方程式に含まれる未知関数の導関数の最高階数を微分方程式の階数という。例えば、y''=yは1階、y''+y=0は2階の微分方程式である。
n階の微分方程式の解でn個の任意定数をもつものを一般解、任意定数に特別の値を与えたものを特殊解という。特殊解でないものを特異解という。
例1 微分方程式
の場合、y=C₁cosx+C₂sinxは一般解。この一般解にC₁=1、C₂=0を与えたy=cosxは特殊解。
例2 微分方程式
の場合、y=Cx+C²は一般解、は特異解。
y(x)についての1階の微分方程式の一般形は
である。
特に、について解かれているとき正規形という。すなわち、
また、(2)式のG(x,y)がxだけの関数φ(x)とyだけの関数ψ(y)の積φ(x)ψ(y)である場合、変数分離形という。すなわち、
例3
はdy/dxについて解かれていないので正規形でなく、非正規形である。
これをdy/dxについて解いた
は正規形。
は、xだけの関数φ(x)=1/xとyだけの関数の積ψ(y)=yの形になっているので、変数分離形である。
変数分離形
の解は
問題1 次の微分方程式を解け。
【解】
(1)
(2)
両辺を(1+x²)(1+y²)で割ると
は定数だから
とおくと、
(解答終)
例えば、次の微分方程式があるとする。
これは、x+y=tとおき、この両辺をxで微分すると、
これを(4)式に代入すると、
と一般形を求めることができる。
この微分方程式のように、変数を置き換えことによって、微分方程式を変数分離形に変換することができる場合がある。
ベクトル関数の回転 [ネコ騙し数学]
ベクトル関数の回転
ベクトル関数A(x,y,z)の成分をとすると、
を成分とするベクトルをAの回転といい、記号
などであらわす。
すなわち、
行列式を用いてあらわせば、
である。
したがって、ハミルトン演算子∇をベクトルと考えれば、∇×Aは∇とAの外積と考えることができる。
問1 原点からの位置ベクトルをrとするとき、∇×r=0であることを示せ。
【解】
(解答終)
問2 φ(x,y,z)をスカラー関数とすれば、
であることを示せ。
【解】
よって、スカラーポテンシャルの回転は零ベクトル0である。
(解答終)
問3 A(x,y,z)をベクトル関数とすれば、
であることを示せ。
【解】
(解答終)
ベクトル場Aがベクトル関数pの回転で表されるとき、すなわち、
のとき、pをAのベクトルポテンシャルという。問3より、ベクトルポテンシャルをもつベクトル場の発散は0である。
関数空間と距離の初歩の初歩 [ネコ騙し数学]
関数空間と距離の初歩の初歩
Cを有界閉区間[a,b]で連続な関数のすべてを集めた集合とし、記号C[a,b]で表すことにする。
fとgを[a,b]で連続な関数とすると、
だにゃ。
そうすると、[a,b]で
は連続だから、|f(x)−g(x)|は[a,b]で最大値を必ずもつ。
そこで、
と、d(f,g)を定義する。
(1)式のは、[a,b]での関数の最大値のこと。
さてさて、(1)のように定義すると、
また
であることは明らかだろう。
さらに、
も明らかだろう。
h∈C[a,b]とするとき、三角不等式から
したがって、
つまり、(1)のように定義すると、次の距離の公理をすべて満たす。
(1)式で、有界閉区間[a,b]で連続な関数の距離を定義できるというわけ。
また、距離の公理の条件(ⅰ)〜(ⅲ)を満たすものならば、どれを距離に選択してもよい。
オレは(1)式の距離の定義は嫌いだ。だから、f,g∈C[a,b]の距離を
と定義したい。
いいにゃ、いいにゃ、素晴らしいにゃ。
――ただし、(2)を使いたいならば、(ⅰ)〜(ⅲ)を満たしていることを証明してから使うこと!!――
我々が通常、距離と呼ぶものは、ユークリッド距離と呼ばれるもので、数ある距離の一つにしか過ぎない。
 問題1 [0,1]で定義された関数f(x)=x²とg(x)=xがあるとする。(1)式で定義された距離d(f,g)を求めよ。
問題1 [0,1]で定義された関数f(x)=x²とg(x)=xがあるとする。(1)式で定義された距離d(f,g)を求めよ。
【解】
[0,1]ではx²≦xだから、
したがって、x=1/2のとき、最大値は1/4。
よって、fとgの距離d(f,g)は
(解答終)
問題2
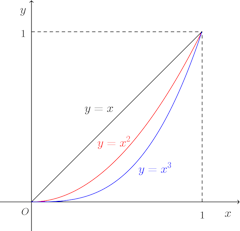
(1) 閉区間[0,1]で定義される関数f、g,hが、f(x)=x²、g(x)=x、h(x)=x³であるとき、
が成立することを確かめよ。
(2) 次のことを証明せよ。
ベクトル関数の発散 [ネコ騙し数学]
ベクトル関数の発散
ベクトル関数A(x,y,z)のx、y、z成分をとする。すなわち、
とする。
このとき、
をベクトル関数Aの発散と言い、記号
などであらわす。
すなわち、
である。
ハミルトン演算子∇は
だから、ベクトル関数Aの発散∇・Aは
と、ハミルトン演算子∇とベクトル関数Aの内積と考えることができる。
問1
の発散を求めよ。
【解】
![]()
(解答終)
問2 原点に対する位置ベクトルをrとするとき、次の発散を求めよ。
【解】
(1)
だから、
(2) のx成分を
とすると、
。
同様に、
よって、
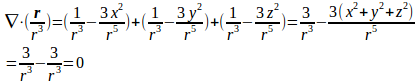
(解答終)
なお、
は暗記物!!
ベクトル関数Aが
の発散は、
である。
と書き、
とおけば、これは微分演算子∇²をφに作用させたものと考えることができるから、
∇²をラプラス演算子、ラプラシアンと呼び、∇²のかわりに記号Δを使うこともある。
また、微分方程式
![]()
はラプラス方程式と呼ばれ、これを満足する関数を調和関数という。
問3 原点からの距離をrとすると、
であることを示せ。
【解】
同様に、
したがって、
問2より
よって、
(解答終)
問3より、
は、ラプラス方程式∇²=0を満たすので、調和関数である。
スカラー関数の勾配と方向微分係数 [ネコ騙し数学]
スカラー関数の勾配と方向微分係数
定点Pと単位ベクトルuが与えられたとき、Pを通りuを方向ベクトルとする直線をCとする。直線C上の点Qのパラメータとして点Pからの距離をsをとると
である。したがって、点Qの位置ベクトルをr(s)とすると、
である。
極限値
が存在するとき、この極限値を点Pにおけるfのu方向の方向微分係数といい、記号
などであらわす。
したがって、点Pにおける、fのu方向の方向微分係数は、点Pにおけるfの勾配ベクトルとuとの内積に等しい。∇fとuのなす角をθとすれば、
よって、θ=0のとき、は最大値|∇f|をとる。
ゆえに、点Pにおける勾配∇fは、点Pにおける曲面f(x,y,z)=cに垂直で、fの増加する向きに向かい、その大きさは、曲面f(x,y,z)=cの法線方向に対する増加率に等しい。
ベクトルと∇fとの内積は
だから、
と書き
とおけば、これは一種の微分演算子で、これをfに作用させたものがと考えられるので、
と書くことができる。
したがって、fのu方向の方向微分係数は
と書くことができる。
問1 点(1/2,1/2)における
の(−1,1)方向の方向微分係数を求めよ。
【解】
(−1,1)方向のベクトルの単位ベクトルuは
また、
より、点(1/2,1/2)におけるf(x,y)の勾配は
![]()
だから、点(1/2,1/2)におけるf(x,y)の方向微分係数は
(解答終)
問2 関数fを
とする。
(1) ∇fを求めよ。
(2) 点(1,0)におけるπ/3方向の方向微分係数を求めよ。
(3) 点(1,0)における方向微分係数が最大になる方向の基本ベクトルを求めよ。
【解】
(1)
したがって、
(2)
x軸と方向ベクトルのなす角をθとすると、θ=π/3方向の単位ベクトルuは
したがって、点(1,0)におけるπ/3方向の方向微分係数は
(3) 方向微分係数が最大になるのは、単位方向ベクトルuが∇fが同方向のとき。点(1,0)における関数fの勾配∇f=(2,0)だから、単位方向ベクトルu=(1,0)のとき、すなわちθ=0方向のときに最大になる。
(解答終)
なお、方向単位ベクトルu=(cosθ,sinθ)のとき、f(x,y)の点Pにおける方向微分係数は
となる。
問3 φ=φ(x,y,z,t)において、x、y、zがtの関数であるとき、
であることを示せ。
【解】
rを点P(x,y,z)の位置ベクトル
とすると、
したがって、
![]()
(解答終)
rを動点Pの位置ベクトルとすると、速度ベクトルvは
だから、
![]()
これは、流体力学や連続体力学で実質微分や物質微分と呼ばれるものである。
スカラー関数の勾配 [ネコ騙し数学]
スカラー関数の勾配
関数φ(x,y)がC¹級であればf(x,y)は全微分可能で
![]()
あるいは、Δx、Δyをdx、dyに置き換え
で表される。
このとき、ベクトルを関数φの勾配(gradient)といい、記号
などであらわす。すなわち、
![]()
である。
したがって、
とすると、全微分dφは、ベクトルの内積を用いて
とあらわすことができる。
φ(x,y)=c(一定)とすれば、φ(x,y)=cは1つの曲線をあらわす。この曲線上の点P(x₀,y₀)における全微分は
![]()
であり、これは点Pにおける曲線φ(x,y)=cの接線の方程式である。
したがって、
とおけば、曲線φ(x,y)=cの点P(x₀,y₀)における接線の方程式は
となり、これは∇φが曲線φ(x,y)=cと直交していることを表している。つまり、∇φは曲線φ(x,y)=cの法線ベクトルである。
この議論は、そのまま、2次元から3次元へ拡張することができ、C¹級の関数φ(x,y,z)に対して、φの勾配を
を定義する。
そして、
をハミルトン演算子といい、記号(微分演算子)∇をナブラと読む。
曲面φ(x,y,z)=cの点P(x₀,y₀,z₀)における接平面の方程式は
![]()
であり、∇φは曲面φ(x,y,z)=cと直交する。そして、∇φはこの曲面の法線ベクトルである。
特に、z=f(x,y)のとき、φ=f(x,y)–z だから、
曲面z=f(x,y)の点P(x₀,y₀,z₀)における接平面の方程式は、
である。
問 z=x²+xy+2y²の点(1,1,4)における接平面の方程式を求めよ。
【解】
だから、
よって、
(解答終)
なにか冗漫でスッキリしないな。次のように書くべきか。
曲面φ(x,y,z)=cがある。曲面上の点P(x,y,z)を通る曲面上の曲線x=x(t)、y=y(t)、z=z(t)を考えると、φはtの関数である。そこで、tを微分すれば、
である。とすると、
で、これは曲面φ(x,y,z)=cの接線ベクトルである。
したがって、
よって、∇φは曲面φ(x,y,z)=cと直交し、∇φはこの曲面の法線ベクトルである。
問題1 uがx,y,zの関数で、uの関数をf(u)とすれば、
であることを示せ。
【解】
(解答終)
問題2 原点に対する位置ベクトルをrとし、r=|r|とすれば、
であることを示せ。
【解】
(ⅰ) だから、
同様に、
したがって、
(ⅱ)
同様に、
よって、
(別解)
f(r)=1/rとおけば、問題1より
(解答終)
問題3 スカラー関数u(x,y,z)、v(x,y,z)の関数をF(u,v)とするとき、次の式を示せ。
【解】
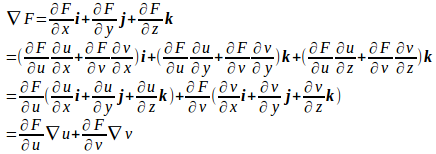
(解答終)
ベクトル関数の偏微分 [ネコ騙し数学]
ベクトル関数の偏微分
ベクトルAが2つのスカラーの関数、すなわち、A=A(u,v)であるとする。
2変数のベクトル関数A(u,v)の偏導関数を
で定義する。
A(u,v)のx成分、y成分、z成分をとすると、
である。
問 ベクトル関数の偏導関数を求めよ。
【解】
Aのx成分、y成分、z成分をとすると、
だから、
したがって、
(解答終)
なんとも見づらいので、ベクトル表示で次のようにしたほうがいいのだろう。
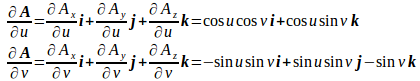
u、vの微小変化Δu、Δvに対して
になるとすれば、Δu、Δvをdu、dvであらわし、
をAの全微分という。
そして、uとvがtの関数、すなわち、u=u(t)、v=v(t)のとき、実関数のときと同様にチェーンルールが成立し
である。
また、uとvがs、tの関数、すなわち、u=u(s,t)、v=v(s,t)のとき
である。
曲面の方程式は、スカラー変数、u、vを用いれば、
であるから、曲面上の任意の点P(x,y,z)の位置ベクトルをとすれば、曲面は
で表される。これを曲面のベクトル方程式という。
vを一定としuを変化させれば、rは曲面上の曲線をあらわす。これをu曲線という。また、uを一定にしvを変化させれば、rは曲面上の曲線をあらわす。これをv曲線という。偏微分係数の定義よりあきらかなように、はu曲線の接線ベクトルであり、
はv曲線の接線ベクトルである。
また、u、vが変数tの関数であるときには、は曲面上の曲線をあらわす。曲面上の点Pにおける接線ベクトルは
したがって、Pを通る曲面上の曲線の接線は、が定める平面上にある。この平面を点Pにおける接平面といい、Pを通り接平面に垂直な直線を法線、Pを始点とし接平面に垂直なベクトルを法線ベクトルという。したがって、
は法線ベクトルである。
問2 曲面z=1–x²–2y の点(1,1,−2)における接平面を求めよ。
【解】
x=u、y=vとおくと、z=1–u²–2v。よって、曲面上の点の位置ベクトルは
だから、
法線ベクトルnは
点(1,1,−2)のときu=x=1、v=y=1だから、(1,1,−2)における法線ベクトルnは
したがって、曲面z=1–x²–2y の点(1,1,−2)における接平面の方程式は
(解答終了)
曲面z=f(x,y)上の点P(x₀,y₀,z₀)における接平面の方程式は
である。
これを使うのならば、
となるので、接平面の方程式は
ベクトルの微分の問題 [ネコ騙し数学]
ベクトルの微分の問題
問題1 曲線上を運動する質点Pの原点に対する位置ベクトルをr、曲線上の定点からPまでの曲線の長さをs、時間をtとすれば、接線ベクトルaの接線成分、法線成分
は
であることをしめせ。
ここで、 、ρは曲率半径とする。
【解】
P点の速度ベクトルvは
よって、
ここで、κは曲率で
したがって、
である。
(解答終)
補足
tは点Pにおける曲線の単位接線ベクトルだから
これを時間tで微分すると、
これからtと、すなわち、
が直交していることがわかる。
問題2 次の螺旋曲線の(単位)接線ベクトル、主法線ベクトル、従法線ベクトル、さらに曲率κと捩率τを求めよ。
【解】
したがって、
よって、
単位接線ベクトルtは
また、
ゆえに、曲率κは
よって、主法線ベクトルnは
従法線ベクトルbは
これから、
となり、捩率τは
(解答終)