第18回 中線定理 [ネコ騙し数学]
第18回 中線定理
§1 中線定理
中線定理は三角関数のところで証明していますが、三平方定理を用いて新たに証明することにします。
中線定理(ハップスの定理)
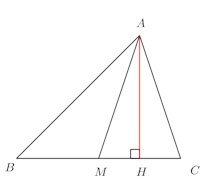
△ABCの辺BCの中点をMとすれば
AからBCに垂線をおろし、交点をHとする。
△ABHは直角三角形なので
△AHCも直角三角形
①と②を足すと、
鈍角三角形の場合(∠C>90°)
図のように、BCの延長線上にAからおろし、その交点をHとする。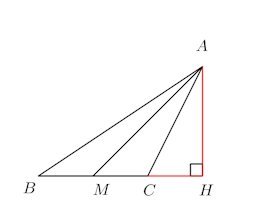
△ABHは直角三角形
よって、
(証明終わり)
なお、次のような直角三角形のとき、中線定理(ハップスの定理)は三平方の定理になる。
ちなみに、他の幾何の定理がそうであるように、逆も成り立つにゃ。
中線定理をさらに一般にしたスチュワートの定理がある。
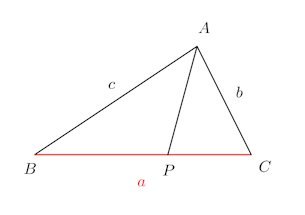
スチュワートの定理
三角形ABCと辺BC上の点Pに対して
§2 問題
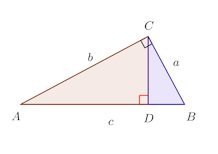
問題1 Aが直頂角の直角三角形ABCにおいて、辺AB、辺ACにそれぞれD、Eをとれば、
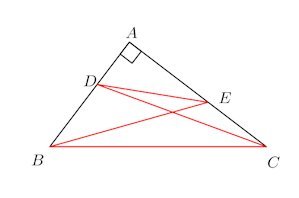
【解】
もういいでしょう。
問題2 二等辺三角形ABCの底辺BC上の1点をDとすれば、次の等式が成り立つことを証明せよ。
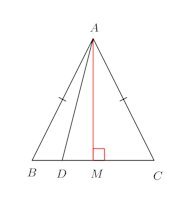
底辺の中点MとAを結び、その交点をMとする。
△ABCは二等辺三角形なのでAM⊥BC
DはBM上にあるとする。△ABMと△ADMは直角三角形なので三平方の定理が成り立ち、
また、
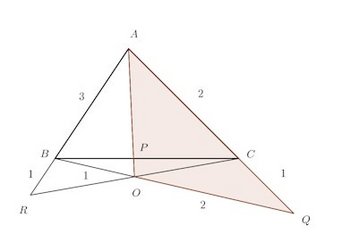
問題3 四角形ABCDの辺AR、BC、CD、DAの中点をそれぞれP、Q、R、Sとするとき、
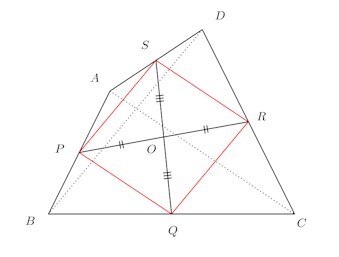
【証明】
四角形PQRSの対角線の交点をOとする。中点連結定理より、
また、同様に中線連結定理から
△QRPに対して中線定理を使うと
また、
①と②より
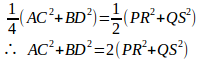
(証明終わり)
第17回 三平方の定理(ピタゴラスの定理) [ネコ騙し数学]
第17回 三平方の定理(ピタゴラスの定理)
§1 三平方の定理
定理 三平方の定理(ピタゴラスの定理)
△ABCにおいて∠C=∠Rならば
逆も成り立つ。
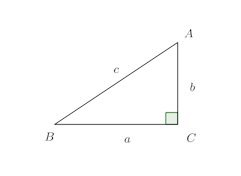
【証明】
この図が証明。
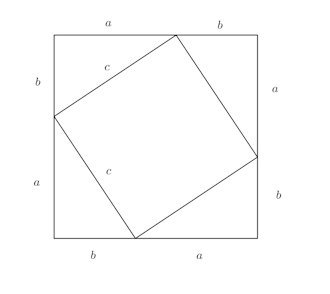
一辺(b+c)の正方形の面積=4×直角三角形ABCの面積+一辺cの正方形の面積
(逆の証明)
B'C'=a、A'C'=b、∠C'=∠Rである△A'B'C'を考える。直角三角形なので
よって、
△ABC≡△A'B'C' (三辺相等)したがって、
∠C=∠C'=∠Rとなり、c²=a²+b²ならば∠C=90°の直角三角形である。
(証明終わり)三平方の定理の逆の証明では、「同一法」と呼ばれる証明法を用いている。
同一法とは、
「pならばq」が真で、かつ、qを満たすものがただ一つならば、「pならばq」の逆命題「qならばp」が成立する
ということを用いて、逆命題を証明する数学の証明法。
三平方の定理の簡単な証明としては、この他に以下のようなものがあります。
点CからABに垂線をおろし、交点をそのDとする。
△ABC∽△ACDだから
あるいは、面積比は相似比の2乗を使って
中学校の教科書に載っている三平方の定理の証明は難しいので、あの証明は駄目だケロ。
では、問題を。
問題1 2辺が6、8である直角三角形は2通りある。それぞれの3辺で残りの辺の長さを求めよ。
【解】2辺が直角を挟み、残りの1辺が直角三角形の斜辺である場合と、そうでない場合の2通りがある。
直角三角形の斜辺である場合、
問題2 直角三角形ABCで、斜辺BCの中点をMとするとき、線分AMの長さをもとめよ。
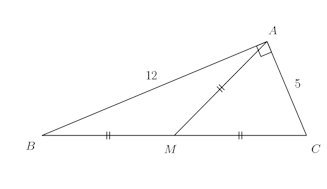
【解】
直角三角形なので、AM=BM=MC。x=AMとすると、BC=2xになるので、三平方の定理より
問題3 四角形ABCDで、対角線が直交するとき、
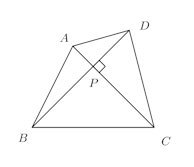
【解】
直角三角形PABで
§2 三平方の定理の平面図形への応用
(1) 座標平面上の2点間の距離座標平面上にある2点A(x₁,y₁)、B(x₂,y₂)の距離ABは
これは、これまでに何度も使ってきたけれど、三平方の定理を使って、このように求められる。
問題4 3点A(2,6)、B(−4,2)、C(0,−4)を頂点とする三角形はどのような三角形か。また、その面積を求めよ。
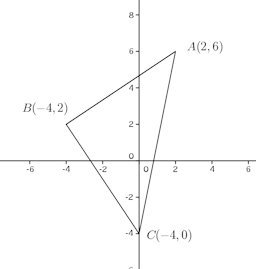
【解】
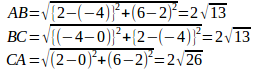
よって、
面積Sは
問題4では
(2) 直交する直線の傾きの積mm'=−1
y=mx+nとy=m'x+n'という2直線があるとする。この2直線が直交するならば傾きの積mm'=−1であり、傾きの積がmm'=−1ならば直交する。このことは、中学や高校で習ったと思う。そして、これは三平方の定理を使って簡単に証明することができる。
傾きだけの問題なので、l:y=mx、l':y=m'xとしても一般性は失われないので、議論を簡単にするために、この場合で考えることにする。
――lとl'との交点が原点Oに一致するように、lとl'を平行移動させたと考えてもいい――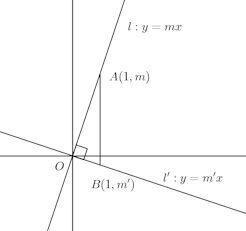
よって、三平方の定理が成り立ち
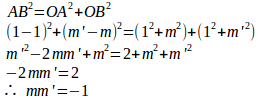
番外編 調和数列 [ネコ騙し数学]
番外編 調和数列
調和平均、調和点列が出てきたので、さらに話を進めて、調和数列。
例えば、6,, 2, 3/2, …
という数の列、数列のように、その逆数が等差数列になる数列を調和数列という。先にあげた
n=1,2,3を代入すれば、こうであることが確かめられる。
ちなみに、が初項y₁で公差dの等差数列であるとき、
だから、
また、の始めの2項がa、bであるとき
等差数列は隣接する二項の差が一定なので
ということで、隣接する三項がa、b、cであるとき、等差数列の場合、
また、a、b、cが調和数列の場合、
問題 直角三角形の3辺の長さa、b、c(cが斜辺)が等差数列をなすとき、a:b:cを求めよ。
【解】
a、b、cが等差数列をなすので、
ということで、明日は「三平方の定理(ピタゴラスの定理)」をやるにゃ。
そして、調和数列、調和点列は、円のところでまた出てくるにゃ。
お前ら、素直に負けを認めたらどうだケロ!! [ネコ騙し数学]
お前ら、素直に負けを認めたらどうだケロ!!
直角も垂直も90°ピッタリだケロ。そして、そして、長方形ABCDも間違いなく長方形。そして、BCの垂直二等分線も正確に垂直二等分線だケロ。
さらに言うと、△A'BP≡△DCPも間違っていない。この三角形は間違いなく合同だケロ。
騙しは、A'Dの垂直二等分線FPにある。
∠A'FP=90°だけれど、あの図では
A'F>FD
になっているんだケロ。
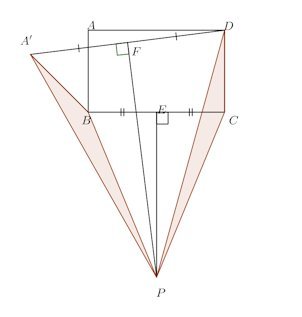
この図のままで正確な図を書くと点Pがずっと下になるので、わかりやすくするために∠A'BAをこの図よりも大きくするにゃ。
そうすると、こうなるにゃ。であるのが分かるだろう。
そして、あの証明は⑥までは正しいんだケロ。
だから、いくら、証明を見て間違いを探そうとしても無駄だと言ったんだケロ。
間違っているのは、図なんだケロ。
そして、上の図を見ながら間違いを探そうとしても、まず100%間違いを見つけることができないのであった。
勝利の踊りをするにゃ。
この人を愚弄したかのような表情がいいケロ。
この記事を読んだ人は、ネムネコへのお賽銭をお忘れなく。
番外編 直角は直角より大きく、かつ、等しいことの証明 [ネコ騙し数学]
番外編 直角は直角より大きく、かつ、等しいことの証明
ネムネコが、スゴイ証明を一つ紹介するにゃ。
今日から数学が変わってしまうかもしれない、すごい証明だケロ。【証明】
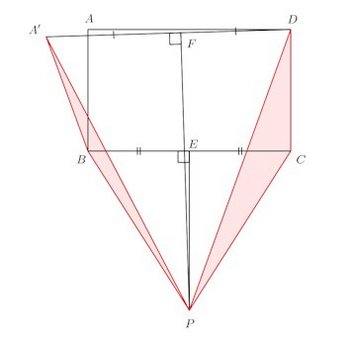
図のように、長方形ABCDの外部に
BCの垂直二等分線とBCの交点をE、A'Dとその垂直二等分線の交点をFとする。
A'F=FDでFPは共通なので、三平方の定理から
同様に、
よって、直角は直角より大きく、かつ、直角に等しい!!
(証明終わり)
△A'BP≡△DCPで、この2つの三角形が合同であること自体、驚きなのに、さらに、とんでもないことが起きてしまった(^^ゞ
この2つの三角形が合同に見えないのは、目の錯角だね(^^)今日から数学史が変わる(^^ゞ
もちろん、この証明には致命的な間違いがある。
――騙しが入っている――
第16回 相似と比例に関する総合問題 [ネコ騙し数学]
第16回 相似と比例に関する総合問題
これまでやってきた図形の相似に関する総合的な問題を、復習をかねて、解くことにします。
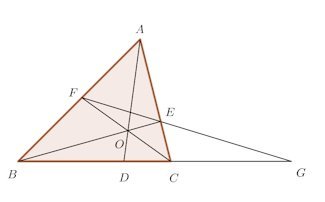
問題1 BC=CG、である。AF=3、EF=2、FC=2のとき、x、yの大きさを求めよ。
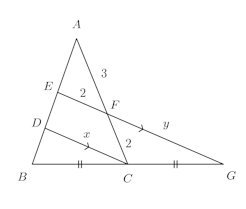
【解】
△ADC∽△AEFだから
題意より
⑨のところは、BC=CG、だから、中点連結定理よりDはBEの中点、そして、EF=2DCとなるので、これを使ってもいい。
この問題で点Dが与えられていなければ、メネラウスの定理を2度使って求めてもよい。
【別解】△ABCとBGでメネラウスの定理より
問題2 である。AB=4、EF=9とするとき、CDの長さを求めよ。
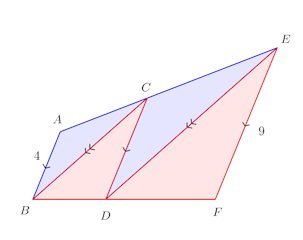
【解?】
台形ABDC∽台形CDFE
と、解いちゃ〜駄目なんでしょうね〜。
【解】
△BDC∽△DFEよって、
だから、
問題3 、ACとBDの交点をO、DB、ACの中点をそれぞれP、Qとし、AD=4、BC=8とするとき、次の問いに答えよ。
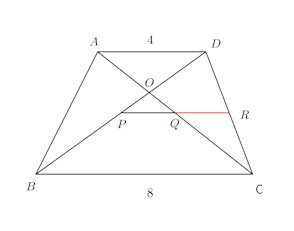
(2) △OADと△OQPの面積比はいくらか。
(3) 四角形ABCDの面積は、△OPQの面積の何倍か。【解】
(1) PQの延長とCDの交点をRとする。
、CP=PBと中点連結定理より、RはCDの中点である。
(2) △OAD∽△OQP。
相似比は
(3) 少しは自分でやるべきだと思うにゃ!!
答えは1/36だケロ。
こんなものは暗算だにゃ。
真面目に解けよな!!
真面目に解いた人にしか、上の式の意味はわからない!!(解答終わり)
PQの長さに関しては、中点連結定理のあたりで
問題4 平行四辺形の中点をE、AEとBDの交点をFとする。平行四辺形の面積が200であるとき、次の問いに答えよ。
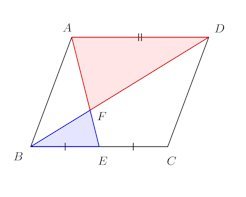
(1) BF:FDを簡単な整数比であらわせ。
(2) △BEFの面積を求めよ。
(3) 四角形DFECの面積を求めよ。【ヒント】
(1) △AFD∽△EFB(2) △ABDは平行四辺形ABCDの面積の半分。さらに、
(3) 100−△BEFだケロ。
オレが解いてもしょうがないケロ。
第15回 調和点列 [ネコ騙し数学]
第15回 調和点列
同一直線上にA、B、P、Qがあって、P,QがABを同じ比に内分、外分、すなわち
AP:PB=AQ:QBのとき、P、QはABを調和に分けるといい、4点A、B、P、Qはこの順に調和点列をなすという。
分かりづらいと思うのですが、A、B、P、Qは図のような位置関係になります。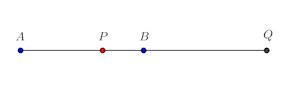
AP:PB=AQ:QB=2:1
の場合について示したものです。式を少し変形すると
問題1 4点、A、B、C、Dが調和点列ならば
【証明】
AB=b、AP=p、AQ=qとする。そうすると、PB=b−p、BQ=q−bになる。
A、B、C、Dは調和点列をなしているので、②より
前に調和平均について少し話したけれど、このことからbはpとqの調和平均になっていることが分かる。
第10回と第11回で次の定理を紹介したにゃ。
定理 △ABCにおいて∠A(またはその外角)の2等分線が対辺(またはその延長)で交わる点をDとすると、
BD:DC=AB:ACである。
△ABCにおいて∠Aの2等分線とBCの交点をP、また、∠Aの外角の2等分線とBCの延長との交点をQとする。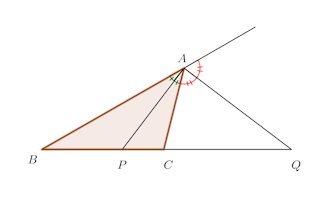
問題2 △ABC内に1点Oをとり、AO、BO、COが対辺と交わる点をそれぞれD、E、Fとする。
△ABCと点Oについてチュバの定理を用いると
(証明終わり)
第14回 問題演習 [ネコ騙し数学]
第14回 問題演習
問題1
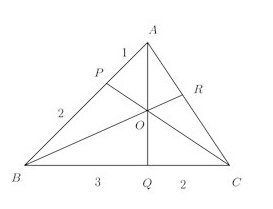
△ABCがある。辺ABを1:2に内分する点をP、BCを3:2に内分する点をQ、直線AQと直線CPの交点をOし、点B、Oを通る直線とCAの交点をRとする。(1) CR:RAを求めよ。
(2) QO:OAを求めよ。
(3) △OBQ:△ABCを求めよ。【解】
(1) チュバの定理より
よって、CR:RA=4:3
(2) メネラウスの定理より
(3) △OBCと△ABCは底辺BCが共通なので、その面積比は
問題2 ∠A=∠Dである2つの三角形、△ABC、△DEFがある。このとき、面積比は
【証明】
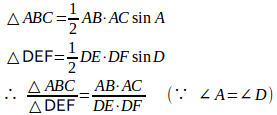
(証明終わり)
確かにそうなのですが、次の図を参考に線分比から証明して欲しいにゃ。
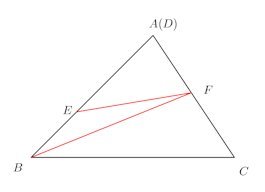
と、思ったけれど、付き合いが長いにゃ、オレには、「こいつらは絶対にやらない」という確信があるにゃ。
だから、不本意だけれど、やるにゃ。
△AEFと△ADBは、AE、ABを底辺と考えると、高さが共通だから、その面積比は
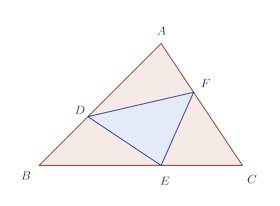
問題3 △ABCの辺BC、CA、AB上にそれぞれ点D、E、Fをとり、
△ABCから薄い紫色の部分を引いたものが△DEFだケロ。
△ABCと△ADFに注目すると
問題4 △ABC内の任意の点をOとし、AO、BO、COの延長と対辺との交点をD、E、Fとするとき、次の等式を証明せよ。
(1)
(2)
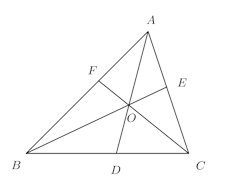
【解】
(1) △ABCと△OBCの底辺をBCとすれば、その面積比は
(2)
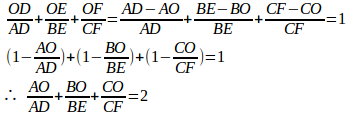
(解答終わり)
第13回 メネラウスの定理とチュバの定理 [ネコ騙し数学]
第13回 メネラウスの定理とチュバの定理
§1 メネラウスの定理
メネラウスの定理
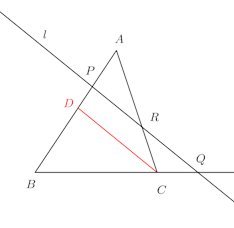
△ABCの辺AB、BC、CAまたはその延長が、1つの直線とそれぞれP、Q、Rと交わるとき
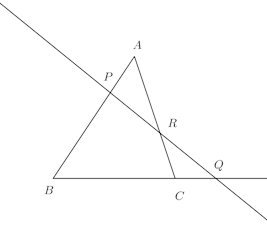
【証明】
CDと直線lは平行なので、
定理(メネラウスの定理の逆)
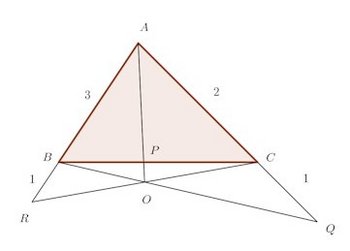
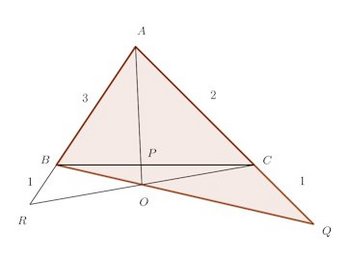
△ABCの辺AB、BC、CAの延長上、または、それらの延長上と2つの辺上にそれぞれP、Q、Rがあり、
【証明】
図のように、
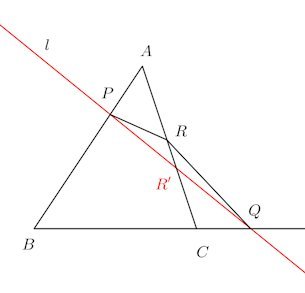
PとQを結ぶ直線lとACの交点をR'とする。
メネラウスの定理より
①と②より
辺CAの内分比が同じ点なのでR=R'で、①のとき、P、Q、Rは1直線上にある。
こういう証明は、背理法のほうがスッキリするのではないか。
そして、この証明に使用した図は背理法を意識したもの。こう書く以外に図の書きようがないケロ!!§2 チュバの定理
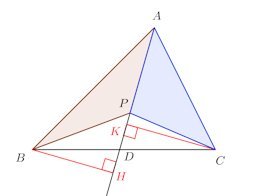
チュバの定理の証明に入る前に、まず、次の図に示される△ABPと△ACPの面積比を考えることにする。
また、△DBH∽△DCKだから、
定理(チュバの定理)
△ABCの辺上にない1点P、A、B、Cとを結ぶ直線が、それぞれ、対辺またはその延長と交わる点をそれぞれD、E、Fとすると、
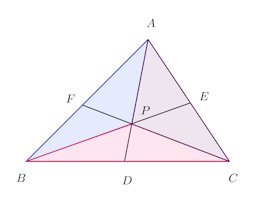
【証明】
△ABPと△ACPとはAPを共有しているので
なのですが、これはメネラウスの定理を使って次のように証明することも可能。
【別証】
メネラウスの定理より、
メネラウスの定理と同様に、チュバの定理も逆が成り立つケロ。
定理 (チュバの定理の逆)
△ABCがあり、辺、BC、CA、ABの辺上に点D、E、Fがあり、
§3 問題
ということで、問題。
問題
BO:OQとAP:POを求めよ。△ABQとRCに注目。
よって、BO:OQ=1:2。
△AQOとRCに注目。
メネラウスやチュバの定理を使えば、このように線分比が求まるという話でした。
第12回 内分と外分 [ネコ騙し数学]
第12回 内分と外分
§1 内分
線分AB上に点Pがあり、AP:PB=m:n (m>0、n>0)となるとき、点Pは線分ABをm:nに内分するといい、点Pを内分点という。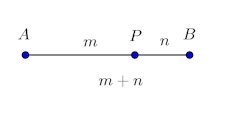
AP:PB=m:nだから、
あるいは、AP:AB=m:(m+n)になるので
A、B、Pが数直線上のA(a)、B(b)、P(p)という点である。
§2 外分
線分ABの延長線上に点Qがあり、AQ:QB=m:n
となるとき、点Qは線分ABをm:nに外分するという。また、この点QをABの外分点という。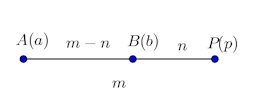
数直線上の点A(a)、B(b)、Q(q)で、a<b、かつ、m>n>0とすると、
形式的な話になるけれど、
そして、
あくまで形式的議論で、こんなものを覚える必要はない。百害あって一利なしなので、
§3 面積比
三角形の面積Sは底辺BC=a、高さをhとすると
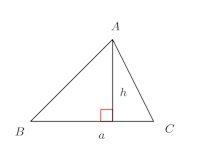
したがって、三角形の面積は、底辺の長さがが一定ならば高さに比例し、高さが一定ならば底辺の長さに比例することがわかる。
【1】 2つの三角形の面積の比は、等底ならば高さの比、等高ならば底辺の比に等しい。
【2】 一辺が共通ならば
【1】について、少し説明すると、等底のときは、△ABCと△A'BCの面積比は
また、高さが一定ならば、△ABDと△ADCの面積比は
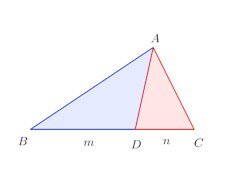
また
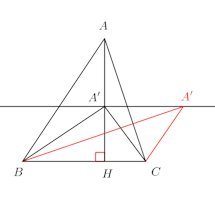
【2】については、次の図を見ると何故こうなるかわかると思う。
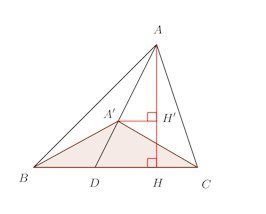
このとき、△ABCと△A'BCの高さの比は
H'H:AH=A'D:AD
になるので、
問題 △ABCの辺BCをm:nに内分する点をDとし、線分ADをp:qに内分する点をA'とする。
次の問いに答えよ。(1) △ABCと△A'BCの面積比を求めよ。
(2) △ABCと△A'BDの面積比を求めよ。【解】
(1) △ABCと△A'BCは底辺BCを共通しているので面積比は
(2) △A'BCと△A'BDは高さが共通。よって、面積比は
面積比を求めることができた。
何でこんなことを急にやり出しかというと、初等幾何で有名なメネラウスの定理とチュバの定理の証明をするためです。