定積分の応用 面積の分割に関する問題

定積分の応用　面積の分割に関する問題

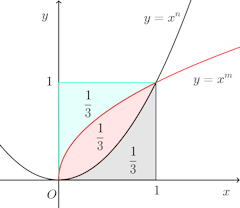
問題１　直交軸において、原点と点(1,1)を結ぶ線分を対角線とする正方形がある。方程式において、nを変えると種々の曲線ができるが、その中から２つの曲線を求めて、これによって正方形を３等分せよ。

【解】

３等分する２つの曲線を

　　

とし、0≦x≦1で

　　

とすると、

　　

よって、

　　

である。

（解答終了）

点(1,1)を点Aとし、原点OとAとを直線で結ぶと、直線OA、つまりy=xに関して対称。

y=x²の定義域を0≦x≦1とすれば、もう一方の曲線はx=y²（0≦y≦1）で、これからy=√xが出てくる。

 

問題２　aを正の定数とするとき、曲線

　　

と両座標軸で囲まれた図形を曲線y=sinxが２等分するようにaの値を定めよ。

【解】

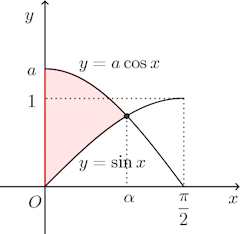0<x<π/2におけるy=acosxとy=sinxの交点のx座標をαとすると、

　　

また、sin²α+cos²α=1だから、cosα、sinαについて解くと
　　

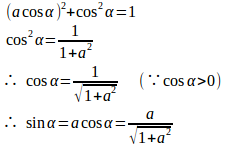
問題の条件より

　　
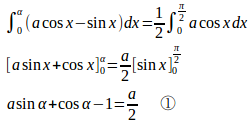
①に
　　
を代入すると、

　　

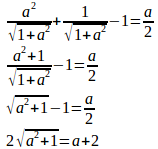
両辺を２乗すると、

　　

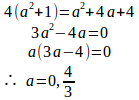
a>0だから、

　　

（解答終了）

 

問題３　曲線y=sinx上の点P(a,b)における接線とx軸との交点をKとし、Pからx軸におろした垂線の足をHとする。

△PKHが曲線y=sinxによって分けられる２つの部分の面積比が

　　（図形PKO）：（図形POH）=1:2

となるようにaを定めよ。ただし、Oは座標の原点、0<a<π/2とする。

【解】

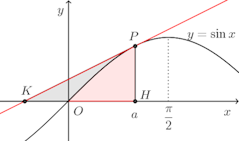図形PKO:図形POH=1:2だから、

　　△PKH:図形POH=3:2

接点Pにおける接線の方程式は、y'=cosxだから

　　

この接線とx軸との交点Kのx座標をtとすると

　　

よって、△PKHの面積S₁は

　　

図形POHの面積S₂は

　　

S₁:S₂=3:2だから2S₁=3S₂。

よって、①と②より

　　

sin²a+cos²a=1を使って③からsin²aを消去すると、

　　

0<a<π/2だからcosa=1は解として不適なので、

　　

（解答終了）

 

問題４　曲線y=logxとx軸との交点をAとする。また、この曲線に原点Oから引いた接線の接点をB、Bからx軸におろした垂線の足をHとする。

（１）　接線OBの方程式を求めよ。

（２）　線分AH上に１点Pをとり、線分AP、BPおよび曲線ABの囲む面積を△BOHの半分にしたい。Pのx座標を求めよ。

【解】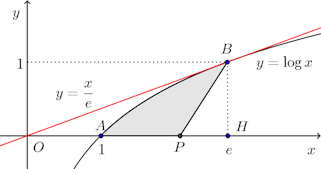

（１）　接点Bの座標を(t,logt）とすると、y'=1/xだから、接線の方程式は

　　

これが原点Oを通過するので、

　　

よって、接線の方程式は

　　

（２）　接点Bの座標は(e,1)だから、△BOHの面積は

　　

点Pの座標をpとすると、△BPHの面積は

　　

問題の条件より
　　

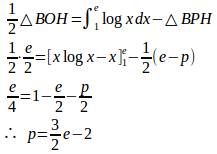
（解答終了）

タグ：微分積分