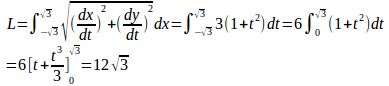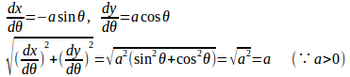積分の応用 曲線の長さ [ネコ騙し数学]
積分の応用 曲線の長さ
§1 曲線の長さ
滑らかな曲線y=f(x)上の2点A(a,f(a))、B(b,f(b))の曲線の長さを考える。下図のように[a,b]を
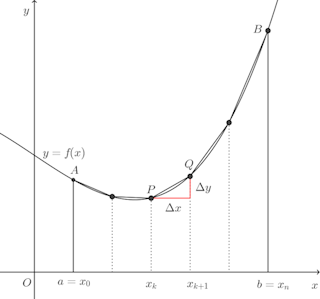
このとき、弧PQの長さl(PQ)は線分PQの長さ
平均値の定理より
すなわち、
曲線y=f(x)(a≦x≦b)の長さLは
問題1 次の曲線のこの長さを求めよ。
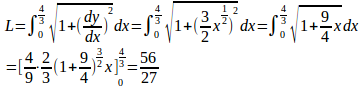
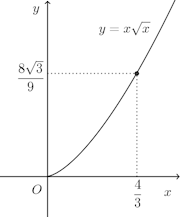
(2)
 したがって、曲線の長さをLとすると
したがって、曲線の長さをLとすると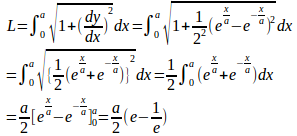
(解答終了)
§2 媒介変数で表された曲線の長さ
媒介変数tで表された曲線
α≦t≦βにおいてf'(t)>0の場合、
よって、媒介変数でx=f(t)、y=g(t)(α≦t≦β)で表された曲線の曲線の長さLは
である。
問題2 媒介変数で表された次の曲線の弧の長さを求めよ。
よって、
![]()
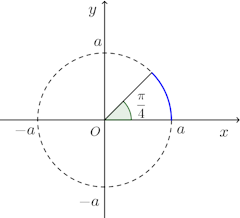
(2) 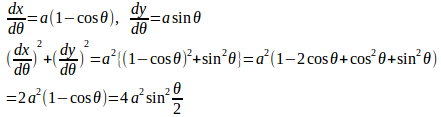
よって
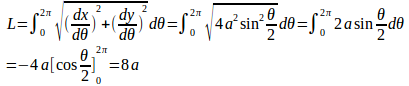
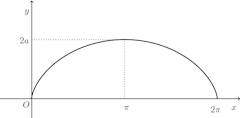
(3)
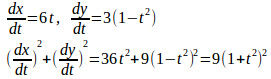
よって