2次精度のルンゲ=クッタ法もなかなか侮れない [ネコ騙し数学]
2次精度のルンゲ=クッタ法もなかなか侮れない
2次精度のルンゲ=クッタ法のプログラムにミスを発見し――修正オイラー法に引きずられて勘違いした(^^ゞ――、プログラムを修正するのと同時に、2次のルンゲ=クッタ法を使って2階の常微分方程式の初期値問題を解くことのできるプログラムをC言語で作ってみた。
そのついでに、
この微分方程式は、単振動、たとえば、バネの運動をあらわす微分方程式で、上の初期条件で解くと、解は次のようになる。
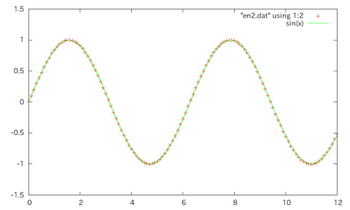
2次精度のルンゲ=クッタ法を用いて、xの増分をh=0.1という数値計算としては、かなり粗い計算を120ステップ計算させてみた。
これがその結果。文句なしの精度で正弦関数を再現出来ていることがわかると思う。
しかも、驚くなかれ、物理でいうところのエネルギー保存則もほとんど満たしている。
この微分方程式は、変数分離法を使って、
そして、上の式は、運動ネルギーとバネの弾性エネルギーの和は一定で変化しないことをあらわしている。
つまり、力学的なエネルギーは不変、保存されるということだにゃ。初期条件、つまり、x=0のとき、y=0、y'=u=1だから、(2)より、
次のように考えることもできる。
さてさて、解いた答えがこの関係を満たしているかどうかだにゃ。
下の図は、2次精度のルンゲ=クッタ法で解いたものを、縦軸にu、横軸にyをとって表したもの。
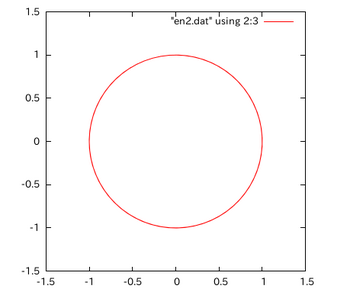
計算結果はほとんど円を描いている。
つまり、エネルギーはほとんど保存されている。数値計算だと、計算を進めるとu²+y²の値は次第次第に増加し、120ステップだから約2周でu²+y²≒1.003まで増加するけれども、分割の幅h=0.1という粗い計算であることを考えると、良好な計算結果と言っていいのだろう。
もっとひどい結果、悲劇的な結果が出ると思っていたので、正直、意外であった。
(修正)オイラー法、ルンゲ=クッタ法で(1)の2階微分方程式を解くには、
この方法については、いずれ、きちんと紹介するにゃ。
実は、4次精度のルンゲ=クッタを用いて2階の常微分方程式の初期値問題を解くBASICのブログラムは1年以上前に紹介しているのだけれど、あのときには理論的な話を一切しなかったので、そういった話をすこし含めて話すつもりでいるにゃ。
あくまで予定だにゃ。
そのための準備を少しずつしている。C言語で申し訳ないけれど、計算に使ったプログラムは次の通り。
(1)以外の問題でも解けるように、汎用性を持たせてある。
#include <stdio.h>
#include <math.h>doublef(double x,double y,double p) {
return -y;}
double g(double p) {
return p;}
void RungeKutta2(double x, double y, double p, double h, int n) {
double k11, k12, k21, k22;int i;
printf("%f %f %f %f \n",x,y,p,y*y+p*p);
for (i = 1 ; i <= n; i++) {k11= h*g(p);
k21= h*f(x,y,p);k12= h*g(p+k21/2);
k22= h*f(x+h/2,y+k11/2,p+k21/2);x=x+h;
y=y+k12;p=p+k22;
printf("%f %f %f %f \n", x,y,p,y*y+p*p);}
}main() {
double x,y,h,p;int n;
n=120;
h=0.1;x=0;y=0;p=1;
RungeKutta2(x,y,p,h,n);}
ちなみに、このプログラムでいじっていいのは、
doublef(double x,double y,double p) {
return -y;}
の黄色の部分と、main() {
double x,y,h,p;int n;
n=120;
h=0.1;x=0;y=0;p=1;
RungeKutta2(x,y,p,h,n);}
の黄色の部分だけです。
間違っても、ルンゲ=クッタ法の計算の本体だけはいじらないでください。
ここをいじると、大変な事になるので注意してください。