定積分の応用 立体の体積 [ネコ騙し数学]
定積分の応用 立体の体積
§1 立体の体積
(1) 回転体の体積曲線y=f(x)(a≦x≦b)をx軸のまわりに回転した体積を、x=g(y)(α≦y≦β)をy軸のまわりに回転した体積を
とすると、
(2) 一般の立体の体積
座標xにおけて軸に垂直な切断面の面積がS(x)ならば、この立体のa≦x≦bの間の体積Vは
§2 問題編
問題1 次の問いに答えよ。
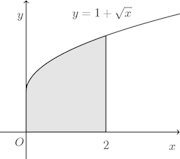
(1) y=1+√x、y=0、x=0、x=2の囲む部分をx軸のまわりに回転して得られる立体の体積を求めよ。(2) y=sinxとx軸とx=0およびx=πの囲む部分をx軸のまわりに観点して得られる立体の体積を求めよ。
(3) 曲線y=logxとx軸およびx=eで囲まれる部分をx軸のまわりに回転して得られる立体の体積を求めよ。【解】
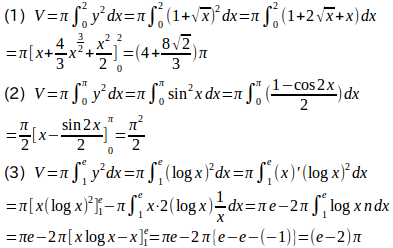
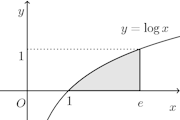
(解答終了)
問題2 次の問いに答えよ。
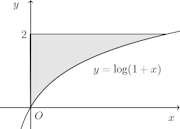
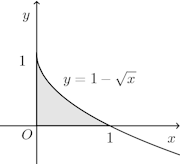
(1) y=log(1+x)、y=2、y軸で囲まれた部分を、y軸のまわりに回転して得られる立体の体積を求めよ。(2) y=1−√xと両軸の世の部分で囲まれた部分をy軸のまわりに回転して得られる立体の体積を求めよ。
【解】
問題3 y=2sinxとy=1(π/6≦x≦5/6π)の囲む部分をy=1のまわりに回転して得られる立体の体積を求めよ。
【解】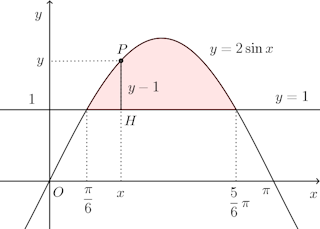 曲線y=2sinx上の動点Pの座標を(x,y)とし、Pからy=1に下ろした垂線の足をHとする。
曲線y=2sinx上の動点Pの座標を(x,y)とし、Pからy=1に下ろした垂線の足をHとする。
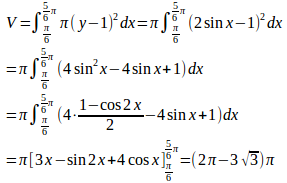
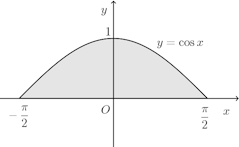
問題4 曲線y=cosx(−π/2≦x≦π/2)とx軸とで囲まれた図形が、x軸のまわりに回転してできる立体の体積V₁を求めよ。また、この図形をy軸ののまわりに回転してできる立体の体積V₂を求めよ。
 【解】
【解】 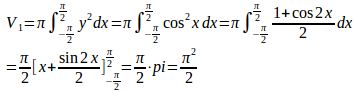
y軸のまわりに回転して得られる体積V₂は
したがって、
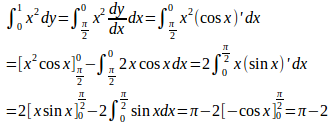
よって、