定積分の応用 体積の変化とその割合 [ネコ騙し数学]
定積分の応用 体積の変化とその割合
問題1 ある容器に、体積Vの水を入れると、水の深さが√Vになる。この容器に水の深さがhになるまで水を入れるとき、その水面の面積を求めよ。
【解】水の深さがyのときの水の体積をV(y)、水面の面積をS(y)とする。
問題の条件より、y=√Vだから
深さyのときの断面積S(y)がS(y)=2yだから
問題2 放物線y=x²をy軸のまわりに回転してできる曲面を内面とする容器がある。毎秒50πの割合で注水するとき、100秒後の水面の上昇速度を求めよ。
【解】t秒後の高さをy、体積をVとすると、
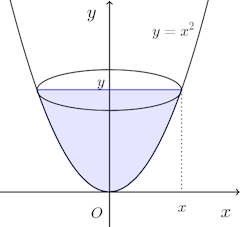 問題3 曲線y=x²(長さはcm)のy軸を軸として回転してできる曲面を内壁とする(回転の軸を鉛直に保つ)に、毎秒vcm³ずつ注入する。水を入れ始めてからt秒後における、次のものを求めよ。
問題3 曲線y=x²(長さはcm)のy軸を軸として回転してできる曲面を内壁とする(回転の軸を鉛直に保つ)に、毎秒vcm³ずつ注入する。水を入れ始めてからt秒後における、次のものを求めよ。
(2) 水面の面積
(3) 水深の増加速度(4) 水面の面積の増加速度
【解】(1) t秒後の水の深さをyとすると、そのときの体積Vは
(2) 水面の面積Sは
(3) (1)より
(4) (2)より
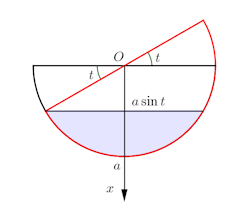 問題4 半径acmの半球形の容器に水がいっぱい入っている。この容器を一定方向に毎分1ラディアンの割合で静かに傾けるとき、
問題4 半径acmの半球形の容器に水がいっぱい入っている。この容器を一定方向に毎分1ラディアンの割合で静かに傾けるとき、
(2) t分後に流れでた水の量を求めよ。
(3) 流れ出る水量の変化率をtの関数としてあらわせ。【解】
(1) 原点Oを中心とする半径aの円の方程式はx²+y²=a²。したがって、右図の水色の部分
(2) 傾ける前の水の量は
(3) 流れ出る水量の変化率は
タグ:微分積分



