定積分の応用 面積3 曲線が媒介変数で表された場合 [ネコ騙し数学]
定積分の応用 面積3 曲線が媒介変数で表された場合
曲線がパラメータで表された場合
次のようにパラメータ・媒介変数で表された曲線
特に、a≦x≦bにおいて、y≧0のとき
問題1 サイクロイド
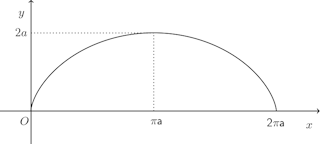
【解】
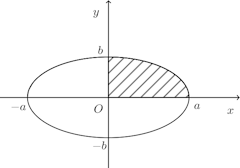
問題2 次の点(x,y)のえがく曲線の囲む図形の面積を求めよ。ただし、a>0、b>0とする。
x=のときθ=π/2、x=aのときθ=0。
よって、
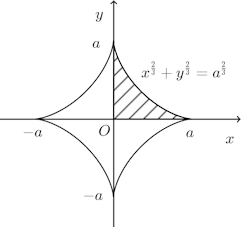
(2) この曲線は
この曲線で囲まれる面積は第1象限の部分を4倍したものに等しい。
上の計算では次の公式を使っている。
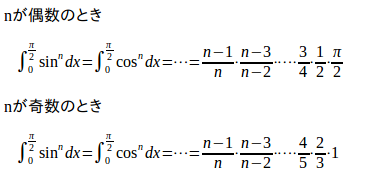
この公式の証明は定積分の漸化式のところで証明をしてある!!
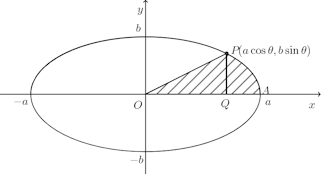
問題3 楕円
弧AP上の点の座標を
求める面積Sは
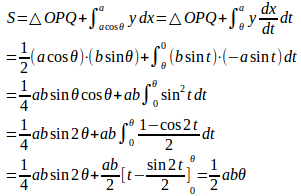
(解答終了)
タグ:微分積分