積分の応用 体積4 パラメータ(媒介変数)で表された図形の体積 [ネコ騙し数学]
積分の応用 体積4 パラメータ(媒介変数)で表された図形の体積
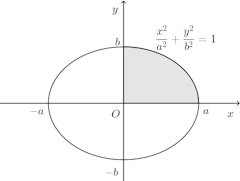 問題1 だ円x=acosθ、y=bsinθによって囲まれた部分をx軸のまわりに回転して得られる立体の体積を求めよ。ただし、a、bは正の実数とする。
問題1 だ円x=acosθ、y=bsinθによって囲まれた部分をx軸のまわりに回転して得られる立体の体積を求めよ。ただし、a、bは正の実数とする。
x=acosθ、y=bsinθから媒介変数θを消去し
しかし、問題1のように媒介変数(パラメータ)を消去して曲線の方程式が求められるとは限らないし、求められたとしても、それが複雑な形で計算に困る場合がある。
そこで、媒介変数を消去するのではなく、置換積分を用いて媒介変数のまま計算し、体積を求めることにする。
体積は
だから、
問題2 次の図形をx軸のまわりに回転してできる立体の体積を求めよ。
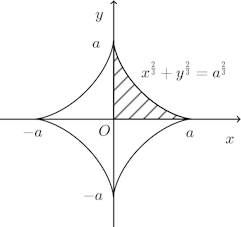
(1) 曲線(アステロイド)
(2) 曲線(サイクロイド)
 【解】
【解】
(1) この図形はy軸に関して対称だから、求める体積Vは第1象限の部分をx軸のまわりに回転して得られる立体の体積の2倍である。
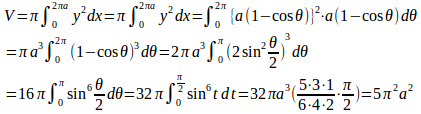
(解答終了)
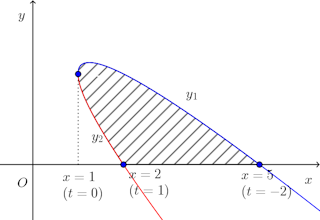
問題3 x=1+t²、y=2−t−t²で表される曲線とx軸とで囲まれる図形がx軸のまわりに回転してできる立体の図形の体積を求めよ。
【解】
この図形は右図のとおり。
この曲線の上側(青い曲線)をy₁、下側(赤い曲線)をy₂とおくと、体積はVは
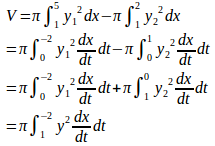
dx/dt=2tだから
問題3の解答が理解できない人は、
タグ:微分積分