関数の極限の復習2 [ネコ騙し数学]
関数の極限の復習2
定理1
とすると
[証明]
(1) c=0のときはあきらか。
c≠0とすると、正数ε>0に対して
となる正数δが存在する。
したがって、
(2)
だから、正数ε>0に対して
となる正数δ₁、δ₂が存在する。
よって、
とすると、
(3)
だから、任意の正数ε'>0に対して適当な正数δをとると
すると、
だから
にとれば、
(4) まず
を証明する。
x→aのときf(x)→lだから、
にとると、
となる正数δが存在する。
このとき
よって
となり(A)が証明された。
そして、(3)と(A)より
(証明終)
関数の極限の復習 [ネコ騙し数学]
関数の極限の復習
高校の関数の極限の定義は、例えば次のようなものである。
高校の関数の極限の定義
aの近くで定義された関数f(x)において、xがaとは異なる値をとりながらaに限りなく近づくとき、f(x)がある一定の値αに限りなく近づく場合、
または
と書き、この値αをx→αのときのf(x)の極限値という。
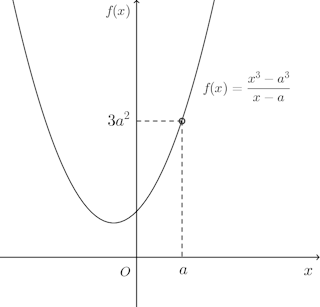
このとき、次の関数のように、関数は必ずしもx=aで定義されている必要はない。
この関数f(x)は、x≠aのとき
となるので、x→aのときのf(x)の極限値は
である。
なのだが、上述の関数の極限の定義は、xがaに限りなく近づくという表現が曖昧ということで、大学数学においては、例えば、次のように関数の極限が定義される。
大学の関数の極限の定義
aの近くで定義された関数f(x)において、任意の正数εに対して、適当な正の数δをとると、
が成り立つとき、
または
で表し、x→aのときf(x)はαに収束するという。また、αをx→aのときのf(x)の極限値という。
そして、この関数の極限の定義が、悪名高いε-δ論法と呼ばれるもので、記号∀、∃を用いて
と簡潔に表現したりする。
問1 ε-δ論法を用いて、次のことを証明せよ。
【解】
(1) 任意の正数ε>0に対して、δ=ε/2にとると、
よって、
(2)
0<|x–1|<δ≦1にとれば
したがって、3δ≦ε、すなわち、δ≦ε/3にとればよい。
よって、任意の正数εに対して
にとれば、
よって、
(2)の別解
0<|x–1|<δのとき
だから、
とおき、これを解くと
したがって、任意の正数εに対して
とδをとると、
となり、よって
(解答終)
問2 ε-δ論法を用いて、次のことを示せ。
【略解】
(1)
![]()
だから、0<δ≦1にとれば
したがって、任意の正数εに対して
となるようδをとればよい。
(2)
![]()
だから、0<δ≦1にとれば
したがって、任意の正数εに対して、
とδをとればよい。
(略解終わり)
第11回 積分の第1平均値の定理、第2平均値の定理 [ネコ騙し数学]
第11回 積分の第1平均値の定理、第2平均値の定理
積分の第1平均値の定理、第2平均値の定理を紹介する前に、(定)積分の平均値の定理を再掲。
定積分の平均値の定理
f(x)が[a,b]で連続ならば、
が存在する。
定積分の第1平均値の定理
f(x)が閉区間[a,b]で連続、g(x)が[a,b]で非負連続ならば、
であるξが存在する。
【証明】
g(x)=0(定数関数)のとき、
だから、a<ξ<bである任意のξに対して
が成立する。
次に、
とする。
f(x)は有界閉区間[a,b]で連続だから最大値Mと最小値mが存在し、
m<Mのとき
よって、中間値の定理より
となるξが存在する。
m=Mのとき、つまり、g(x)が非負で恒等的に0ない定数関数のとき、積分の平均値の定理より
となるξが存在する。
よって、
となるξが存在する。
(証明終)
積分の第2平均値の定理
f(x)を有界閉区間[a,b]で単調かつC¹級、g(x)を[a,b]で連続とする。このとき、
であるξが存在する。
【証明】
とおき、 に部分積分を適用すると
f(x)は[a,b]においてC¹で単調だから、f'(x)≧0またはf'(x)≦0。
よって、積分の第1定理より
となるξが存在する。
したがって、
(証明終)
原始関数と不定積分の定義についてクレームがついた(^^) [ネコ騙し数学]
定積分の第8回で取り上げた「原始関数」と「不定積分」の定義は必ずしも広く世の中で受け入られているものではないから、第9回でクレームがきました(^^ゞ
第8回 原始関数と不定積分
http://nemuneko-gensokyou.blog.so-net.ne.jp/2017-03-25-10
第9回 微積分の基本定理など
http://nemuneko-gensokyou.blog.so-net.ne.jp/2017-03-26-16
敢えてこの定義を採用したのは、(リーマン)積分可能であるけれど、いわゆる原始関数が存在しないものがある、微積分の基本定理が成り立たないものがあることを示すためのもので、特にそれ以上の考えはなかったんだけれど。
高校の数学のように被積分関数が連続である場合、広く世に受け入れられている原始関数、不定積分の定義を採用しても良かったのだけれど、有界閉区間で関数が不連続である点がある場合の積分の場合、この一般的に広く受け入れられている定義だとちょっと塩梅が悪かったものでね。
ちなみに「原始関数」と「不定積分」の定義の混乱事情は、ネット上の以下の記事などを参考にして欲しいにゃ。
http://izumi-math.jp/M_Harada/sekibun/sekibun.pdf
一般に広く採用されている「原始関数」と「不定積分」の定義はコチラ↓だと思うけれど、
http://www.osakac.ac.jp/labs/mandai/writings/Bi1-01m5.pdf
よって立つ立場によって、人によって定義が異なるですよ。
そして、今日、初めて知ったけれど、高校の数学の教科書の「原始関数」と「不定積分」の定義は必ずしも一枚岩ではないようですね。
数学史に疎いので、ネムネコは詳しいことを知らないのだけれど、微分の逆演算としての不定積分――積分定数の違いを無視すればの話――と面積を求める求積法をもとにした定積分とは誕生、発生の経緯が異なっていて、別々の発展を遂げ「微積分の基本定理」によってこの両者が結びついたらしい。
このあたりの件は、たとえば、ここ↓などが参考になると思うにゃ。
https://www.chart.co.jp/subject/sugaku/suken_tsushin/38/38-9.pdf
高校数学では、微分→(微分の逆演算?としての)不定積分→定積分の流れで授業が進められると思うけれど、歴史的には求積法を起源にもつ定積分の方が古いんだケロ。
稲葉三男が『微積分の根底をさぐる』(現代数学社)で書いてあるように
「不定積分を求めることが最終目標であるとすると、(原始関数、不定積分の定義が本によって異なると)、たしかにいわれるとおり困ったことになるであろう。しかし、不定積分を求めることを最終目標とすること自体に問題がある。……」
と開き直る、達観するのも一つの手なのかもしれない(^^ゞ
重箱の隅つつきをしだしたら切りがないからね。
この重箱の隅つつき(?)の例として、
稲葉三男は『微積分の根底をさぐる』の中で伝習的な(不定)積分の公式
を例にあげている。
「右辺を微分すると、明らかにその結果は1/xに等しくなるから、この点に関する限り公式(5)は正しいであろう。しかし、を微分すると、導関数が1/xに等しくなるような関数のものとする限り正しくはない。次のものこそ(5)よりも一般的であろう。
ここに、C₁、C₂は一般に異なる定数である。
(中略)
最後の定義(「となるような関数の一般」)に従うならば、公式(5)は正しくなく、公式(6)こそ正しいものである。」
第10回 微積分の基本定理2 [ネコ騙し数学]
第10回 微積分の基本定理2
定理16
fが区間Iで連続、φが区間Jで微分可能であってφ(x)∈I(x∈J)ならば、
a∈Iと任意のx∈Iに対して
である。
【証明】
とおくと、
また、
(証明終)
(1)と(2)より、
fが区間Iで連続、φとψが区間Jで微分可能であってφ(x)、ψ(x)∈I(x∈J)ならば、
問題1 R上の連続関数f(x)に対して次の導関数を求めよ。
【解】
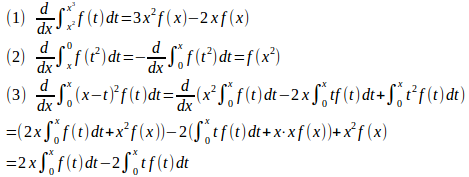
(解答終)
問題2 f(x)は実数Rで連続であって、任意のh∈R、任意のx∈Rに対して
ならば、f(x)は定数関数である。
【解】
xを固定して、
をhの関数と考えてhで微分すると、
任意のhについてf(x+h)=f(x)が成立するので、f(x)は定数関数である(※)。
(解答終)
(※) 任意のxとhについて
が成立するので、
となるので、f(x)は定数関数である。
問題3 f(x)をI=(0,∞)で連続とする。
が任意のx∈I、任意のy∈Iに対して
を満たせば
である。
【解】
xを固定しF(xy)をyの関数と考えて、の両辺をyで微分すると
y=1とすると、
である。
(解答終)