番外編 微分積分の問題を解く５

番外編　微分積分の問題を解く５

問題１　とする。

（１）　f(x)が極値もつようにaの値を定め、極値m(a)を求めよ。

（２）　横軸にa、縦軸にm(a)とし、このグラフをかけ。

【解】

（１）

　　

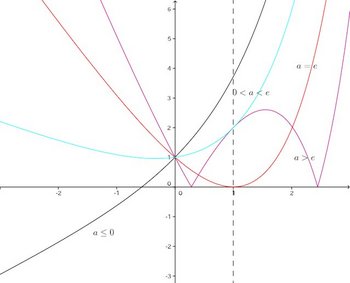
よって、a≦0のとき単調増加となり、極値はない。

a>0のとき、

　　

となり、増減表を書くと次のようになる。

x	…	loga	…
f'(x)	−	0	＋
f(x)	減少	極小　a−aloga	増加

よって、a>0でm(a)=a−alogaになる。

（２）

よって、0<a<1で増加、a>1で減少となり、a=1のときm(a)は極大。

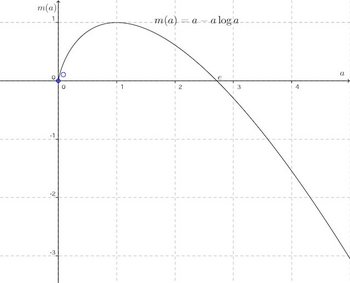
極値の判定は、２階微分をつかって、

（１）　f''(loga)=a>0だから極小

（２）　m''(1)=−1<0だから極大

としてもいいにゃ。

いやまぁ〜、

　　

だから、ほとんど明らかなのだけれど(^^)

 

問題２　方程式の解の個数を求めよ。ただし、aは実数とする。

【解】

x=0は解でないので、

　　

よって、は、y=aとという連立方程式と同値。

で、を調べるために

　　

とし、

　　

よって、x<0で増加、0<x<1で減少、x>1で増加となり、x=1のとき極小。

y=f(x)をグラフにすると、次のようになる。

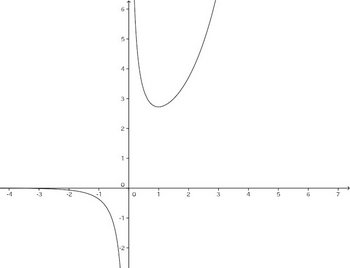
y=aと合せてグラフをかき、y=aとy=f(x)の交点を調べる。

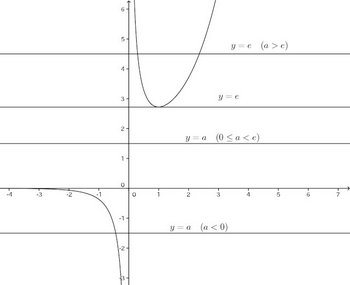
よって、

a<0で解１個

0≦a<eで解なし

a=eで解1個

a>eで解２個

となる。

【別解】

とy=axの交点を調べるにゃ。

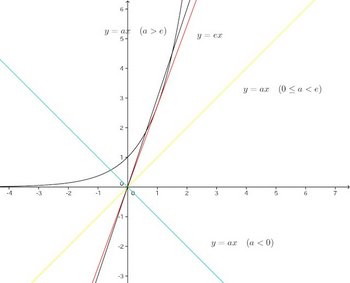
ということで、

a<0で解１個

0≦a<eで解なし

a=eで解1個

a>eで解２個

となる。

【別解２】

問題１の結果を使うにゃ。

とし、y=f(x)とx軸との交点を調べるにゃ。

a≦0ならば、f(x)は単調増加。また、f(−∞)=−∞、f(0)=1で、かつ、f(x)は連続なので、中間値の定理より、f(x)=0を満たすxが−∞<x<0の間に一つ存在する。

a>0のとき、x=logaで極小（最小）。で、極小値a(1−loga)だから、0<a<eのとき、極小値>0となり、f(x)>0となって、y=f(x)はx軸と交わらない。つまり、解はない。
a=eのとき、x=1で最小となり、最小値は0だにゃ。つまり、x=1が解となり、解は１個。
a>eのとき、x=aで最小で、a(1−loga)<0。そして、f(0)=1でx<logaでは単調減少なので、中間値の定理より、0<x<logaの間に解が一つ、さらに、loga<xで単調増加でf(∞)=∞だから、loga<x<∞の間に一つ存在する。

くどくどと説明するより、次のグラフを見れば、このことがわかると思うにゃ。

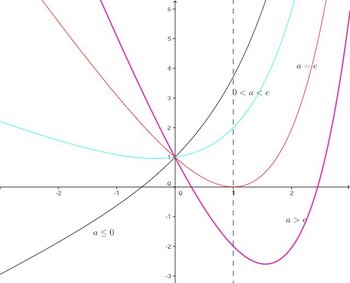
問題３　関数の区間0≦x≦1における最大値が2となるようにaの値を定めよ。ただし、eは自然対数の底である。

【解】

問題１の結果を使うと、a≦eでとなる。

さらに、a≦0ならば、単調増加なのでx=1で最大となる。

　　

となるけれど、a≦0なので、これは不適。

0<a<eのとき、f(x)は0≦x<logaで減少、かつ、loga<x≦1で増加だから、最大値になりうるのはx=0かx=1。f(0)=1なので、f(1)=2とすると、

となる。これは0<a<eという条件を満たすのでよし。

a=eのとき、0≦x<logaで減少なので、f(0)=1が最大値。

a>eのとき、

　　

とすると、

　　

となる。0≦x<αでは減少、α<x<1で増加なので、最大値2の候補はx=0とx=1だけれど、f(0)=1なので、

　　

これは、a>eの条件を満たすので、よし。

ということで、答はa=e−2とa=e+2。

タグ：微分積分