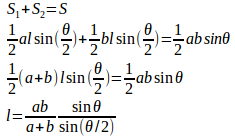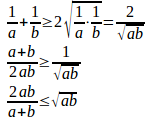番外編 お絵描きの練習 [ネコ騙し数学]
番外編 お絵描きの練習
次の図に示す三角形があるとする。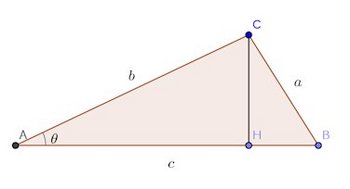
三角形の面積Sは、(底辺×高さ)÷2だから、
そして、CHは三角関数を使うと
だから、
三角形ABCがあるとする。そして、∠Aの二等分線と辺BCの交点をDとし、∠A=θとする。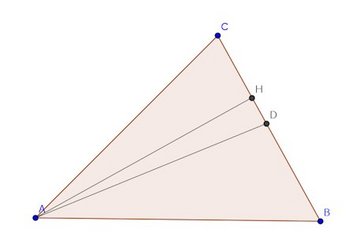
このとき、三角形ABDの面積S₁は
となり、三角形ADCの面積S₂は
だから、三角形ABDと三角形ADCの面積の比は
また、Aから辺BCに垂線をおろし、その交点をHとすると、S₁とS₂は
つまり、∠Aの二等分線は、辺BCをABとACの線分比に分ける。
この重要な性質を知っていたケロか?
三角関数を使わない証明の仕方もあるのだけれど、その証明は初等幾何をやる時に取っておくことにするにゃ。
でも、やりたいのは、これではないんだ。
問題 三角形ABCにおいて、AB=a、AC=b、∠ABC=θ、∠BACの二等分線の三角形内にある部分ADの長さをlとする。
(1) 三角形ABDの面積をa、lとθで表わせ。
(2) lをa、bとθとで表わせ。
(3) a、bを一定に保ち、θを0に近づけるとき、を求めよ。
(1)
(2)
三角形ABCの面積Sは
であり、
ここでやめてもいいのだけれど、
になるので、
としたほうが(3)の極限の計算が楽になる。
(3)
![]()
なお、ここでは三角関数の極限の基本式
そして、ここに出てくる
a>0、b>0のとき、
だから、
つまり、
となる。
相加平均≧相加平均≧調和平均
というわけでにゃ。証明は、
とやってもいいにゃ。