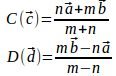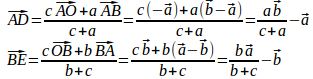第３８回 ベクトルと初等幾何 [ネコ騙し数学]
第３８回 ベクトルと初等幾何
§１ （平面）ベクトル
ベクトルとは、大きさと方向を持った量のこと。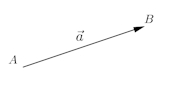
幾何的なベクトルでは、有向線分ABについて、その位置を問題にせず、大きさと方向だけを考えたものをベクトルといい、
とあらわす。
の和
は次のように定義する。
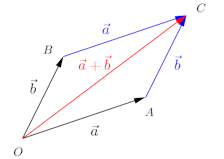
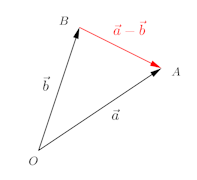
ベクトルの差
は次のように定義する。
ベクトルの内分と外分
位置ベクトルとは原点を始点にするベクトル。２点
であるとき、ABをm:nに内分する点を
、外分する点を
とすると、
これだけあれば、とりあえず、今回、十分でしょう。
§２ 問題
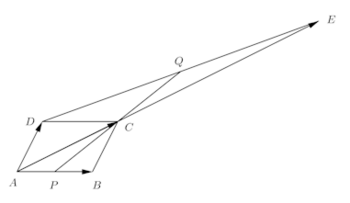
問題１ 平行四辺形ABCDの対角線ACを延長し、延長上に点Eをとって、CE=2ACとなるようにする。また、辺ABおよび線DEの中点をそれぞれP、Qとする。
（１）
を、
であらわせ。（２） ３点P、C、Qは一直線上にあることを示せ。
【解】（１）
（２） 題意より
と
は始点が同じ、かつ、平行なので、P、C、Qは一直線上にある。
ベクトルを使うとこのような解答になるけれど、初等幾何の枠内で解くこともできる。
DAの延長上にAF=ADとなる点をとる（またはPCの延長上にPC=PFとなる点をとる）。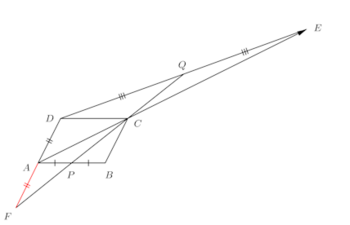
そうすると、条件より、EQ=QD、AC=2CE、さらに、DF=2FAだから、
CFの中点であることは、四角形AFBCが平行四辺形であることより明らか！！
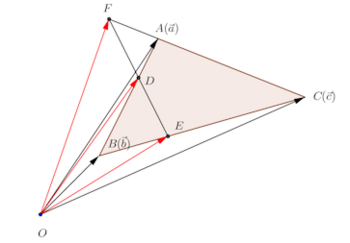
問題２ 
を頂点とする△ABCにおいて、△ABCを1:2に内分する点をD、BCを1:2に内分する点をE、CAを4:1に外分する点をFとする。
（２） D、E、Fは一直線上にあることを証明せよ。
（１）D、E、Fの位置ベクトルを
とする。
（２）
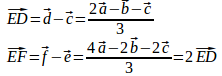
よって、D、E、Fは一直線上にある。
（解答終わり）人間の目というのは当てにならないね。私の目ではFD=DEに見えなけれど、FD=DEです。
それはそれとしまして、この問題は、メネラウスの定理の逆を使うと、
問題３ △OABにおいて、∠AOBの２等分線と辺ABとの交点をC、∠OABの２等分線と辺OBの交点をD、∠OBAの２等分線と∠OAとの交点をEとする。
、OA=a、OB=b、AB=cとする。
（１） 
を
、a、b、cを用いてあらわせ。
（２） 
となるのは、どのような場合か。
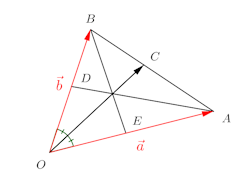
（１） OCは∠AOBの二等分線なので、CはABをa;bに内分する。よって、
（２）は、難しいというよりも、見るからに計算が大変そうなので、パスだにゃ。
第３７回 落穂ひろい [ネコ騙し数学]
第３７回 落穂ひろい
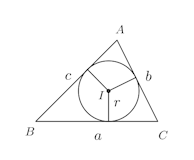
問題１ 三角形の高さをh₁、h₂、h₃、内接円の半径をrとするとき、
【解】
問題２ 三角形の重心をGとするとき、
座標やベクトルの内積を使って解くのが一般的なのだろうけれど、初等幾何の枠内で解くことにする。
その前に、重心と中線定理の復習。重心 三角形の３つの中線は１点で交わり、この交点を重心という。重心は中線を２：１に内分する。
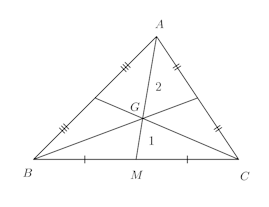
中線定理
三角形ABCにおいて、Aから中線AMを引くと 
この２つを思い出せば、この問題はもう解けたようなもの。
【証明】
重心の性質より、重心Gは中線AMを2:1に内分する。つまり、
問題３ △ABCがあって、AB=2、AC=√3、∠BAC=30°である。
（１） 内接円の半径を求めよ。（２） 内接円と辺ABの接点をDとする。ADの長さを求めよ。
【解】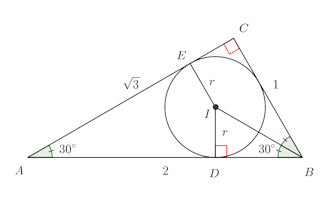
（１） 余弦定理よりBC=1。
よって、△ABCは∠C=90°の直角三角形（∠B=60°）。△ABCの面積Sは
（２） △DBIは∠BDI=90°の直角三角形。Iは内心なので、
あるいは、（２）を次のように解くこともできる。
【別解】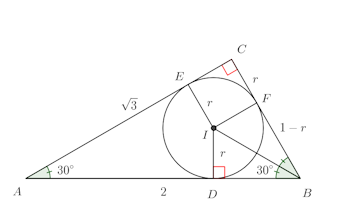
円と２接線の関係より
DB=FBである。
こうすれば、三角関数を使う必要はないね。
（１）で余弦定理よりと書いているけれど、 
だから、
この直角三角形の線分比は中学校で出てくるので、この問題は中学数学の範囲で解くことができる問題であった。
――（２）は少し変えてあるけれど、問題２、問題３は、大昔の大学入試問題です――
