ベクトル ベクトルの内積 [ネコ騙し数学]
ベクトル ベクトルの内積
ベクトルの内積の定義
のなす角（共通の始点がOとなるように平行移動したときにはさむ角）をθとすると、の内積は
で定義される。
なお、
は、それぞれベクトルの大きさをあらわす。
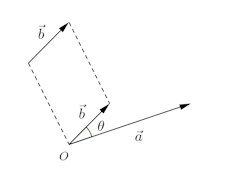
この定義から、次のことがすぐに言える。
また、
のとき
何故ならば、
のとき、２つのベクトルのなす角θ=90°でcosθ=0となり、内積の定義式１より
なので、θ=90°となり、となる。ベクトルの内積については、次のことが成り立つ。
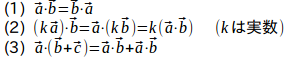
（１）は交換法則、（２）は結合法則、（３）は分配法則であり、これらが成り立つ。
α、β、γが実数とすると、（１） α・β=β・α
（２） (α・β)・γ=α・(β・γ)（３） α・(β+γ)=α・β+α・γ
が成立するので、ベクトルの内積は実数同士の掛け算のように計算をしてよい。
つ・ま・り、内積の計算の仕方がよくわからなかったら、上についている矢印をとって考え、普通の掛け算のように計算をしていい。
ということで、ベクトルの内積に慣れるために、問題を解くことにする。
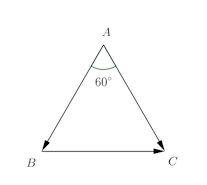
問題１ １辺の長さが１である正三角形ABCがある。
（１） 
の値を求めよ。
（２） 
の値を求めよ。
（３） 
の値を求めよ。
【解】
（１） 
と
のなす角度は60°、また、
。
よって、
（２） と
のなす角は120°。
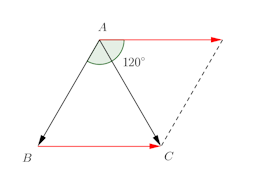
次のように分配法則を使って計算してもよい。
（３） 
と
のなす角は180°だから、
だから、
また、
（解答終わり）
問題２ △ABCにおいて、
とする。
（１） △ABCが正三角形ならば、
（２） （１）の逆は成り立つか。
【解】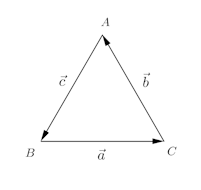
（１） 正三角形ABCの一辺の長さをaとすると
よって、
（２）
ベクトル 位置ベクトル [ネコ騙し数学]
ベクトル 位置ベクトル
原点Oが定まっているとき、点Aの位置は
だから、
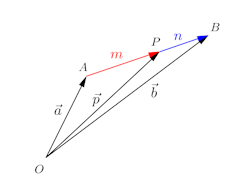
ABをm:nにわける点Pの位置ベクトルを
とすると、
m=nのときは中点で
また、点A、B、Cの位置ベクトルを
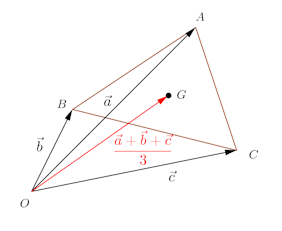
△ABCの重心Gは、BCの中点をMとすると、重心Gは中線AMを2:1に内分する。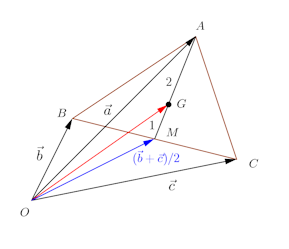
よって、
では、問題を。
問題１ 空間に、同一線上にない３点A、B、Cがある。次の条件を満たすとき、点G、PはA、B、Cに対してどのような位置関係にあるか。
点A、B、C、G、Pの位置ベクトルを
（１）
（２）
（解答終わり）
問題２ 空間に３点O、A、Bがある。点Pが直線AB上にあるための必要十分条件は、次の式が成り立つことであることを証明せよ。
点Pが直線AB上にあるならば、
となり、点Pは直線AB上に存在する。
ベクトル 方べきの定理 [ネコ騙し数学]
ベクトル 方べきの定理
円の方程式のベクトル表示の最後として、方べきの定理に関係する問題を解いてみることにする。
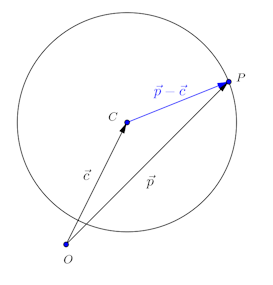
問題１ 平面上に定点Oと半径rの定円Cとがあり、
である。いま、Oを通って円Cと交わる直線lをひき、その交点の一つをPとし、l上の単位ベクトルを
とする。
とrとの関係式を求め、それから得られるtのtの２つの値をt₁、t₂とすると、積t₁t₂はlの方向に関係なく一定であることを示せ。（２） ２の結果の図形的な意味を説明せよ。
【解】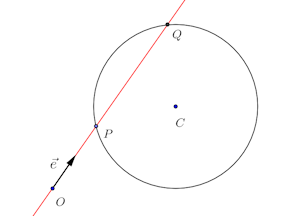
（１） 円の方程式は
、つまり、直線lの方向に関係なく一定である。（２） 方べきの定理！！
（解答終わり）
ベクトルを使うと、このように方べきの定理は証明される。
問題２ 円Cの周上に１点Oがある。いま、Oから出る半直線上にOP・OQ=k（kは正の定数）となるように、２点P、Qをとるものとする。
Pが円Cの周上を動くとき、QはOCに垂直な直線上を動くことを証明せよ。【解】
点P、点Qの位置ベクトルを 
は同方向のベクトルなので
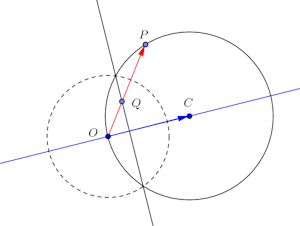
（証明終わり）
（※）
このことはベクトルの成分を使って考えるとがわかりやすい 
ベクトルを使うならば、
そして、この問題は、反転によって原点を通る円はOCに垂直な直線に移されるということの証明になっているのであった。
ベクトル 円の接線の方程式 [ネコ騙し数学]
ベクトル 円の接線の方程式
前回のベクトルを用いた円の方程式に引き続き、ベクトルを用いた円の接線の方程式の表現形式について説明することにする。
原点Oとする平面上の動点Pの位置ベクトルを
とする。この平面上で、中心
、半径rの円 
とすると 
P₁における円Cの満たすべき条件は、
P₁P⊥CPまたはP=P₁である。
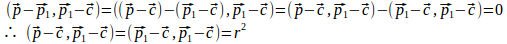
になる。
また、P=P₁のとき、 
よって、点P₁における円Cの接線の方程式は
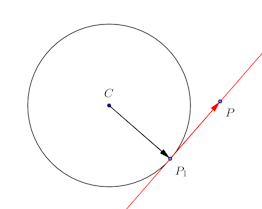
原点Oを中心とする半径rのx²+y²=r²の接点P₁(x₁,y₁)における接線の方程式は
同様に、より一般のC=(a,b)を中心とする半径rの接点P₁(x₁,y₁)における接線の方程式も
ちなみに、
問題 平面上で、
を定点、を動点の位置ベクトルとするとき、
における接線は 
【解】
を直径とする円である。円の中心
は
は円上にあるので
話が後先になってしまったのだけれど、直線ｌ：ax+by+c=0と
とは直交する。
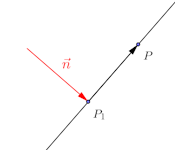
また、に垂直で、点P₁(x₁,y₁)を通る直線の方程式は
で、c=−(ax₁+by₁)とすると
ベクトル 円の方程式 [ネコ騙し数学]
ベクトル 円の方程式
点を中心とする半径rの円のベクトルを用いた方程式は
になる。ここで
は円Cの円周上の点。
円の中心Cが原点の時は
となる。
ベクトルの円の方程式の計算では内積の知識が必須なので、ベクトルの内積の復習。
ベクトルの内積は、ベクトルの大きさを、さらにのなす角度をθとすると
また、内積を
この定義から、
のとき 
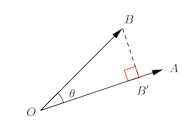
次に、内積の幾何学的な意味について考えることにする。
始点をOとする
という２つのベクトルがあるとする。
つまり、内積は、OAと、OBのOA上への正射影OB'との積と考えることができる。
ベクトルの内積については次のことが成り立つ。
これを見るとわかるけれど、内積は実数同士の掛け算の自然な延長になっている。
だから、普通の実数同士の掛け算のように計算をしてよい。
これで準備は整った。
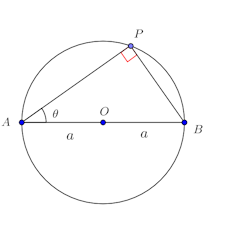
問題を解いてみることにする。問題１ Oを原点とする平面上で、A、B、Cを定点、Pを動点とし、その位置ベクトルを
（１）
（２）
AP⊥BP
のいずれかで、P=A、P=B、∠APB=90°
のどちらかであり、Pの軌跡はABを直径とする円周である。（別解）
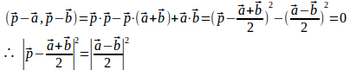
よって、Pの軌跡はABの中点を中心、AB/2を半径とする円周上である。
ここで、
（解答終わり）
少し補足説明をすると、
∠APB=90°のとき、円周角の定理より、点PはABを直径とする円周上に存在することになる。そして、A=P、B=PからA、Bも含まれ、ABを直径とする円になる。問題２ 平面上で、A、Bは定点、Pは動点とする。また、cを正の定数とするとき、つぎの条件を満たす点Pの軌跡を求めよ。
A、B、Pの位置ベクトルを
とする。
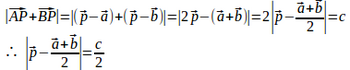
よって、ABの中点を中心とする半径c/2の円周。
（２）
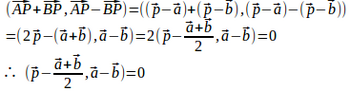
線分ABの中点をCとすると、
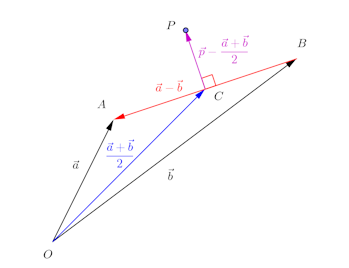
（別解）
第３９回 軌跡のイントロ [ネコ騙し数学]
第３９回 軌跡のイントロ
軌跡とは、ある条件を満たす点の集まり、点の集合のこと。
では、問題。
問題１ 座標平面上２定点A₁(−a,0)、A₂(a,0)がある。この平面上において
【解】
（解答終わり）
このようにして得られる円をアポロニウスの円という。
では、A₁P=A₂Pのときはどうなるか。
ということで、
m≠nのとき アポロニウスの円
m=nのとき A₁(−a,0)とA₂(a,0)の垂直二等分線になりそうだ。
ということで、次の問題。
問題２ m、nが正の数で
m≠nのとき
はの内積をあらわす。ベクトルの内積は、２つのベクトルのなす角度をθとすると
【解】
m≠nのとき 
とし、さらに
とすると、点CとDは、それぞれ、線分ABをm:nに内分する点と外分する点をあらわしている。そして、
m=nのとき
（解答終わり）
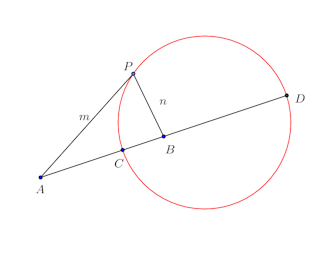
４点A、C、B、Dがこの順にならび同一線上にあるとする。このとき、
AC:CB=AD:DBが成り立つとき調和点列という。
そして、上の問題の証明からアポロニウスの円と調和点列は深い関係があり、
番外編 不等式の証明 [ネコ騙し数学]
番外編 不等式の証明
いきなり、
問題１ a、ｂが実数であるとき、次の不等式を証明せよ。
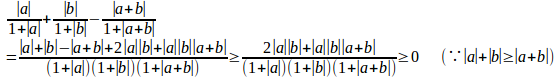
よって、
等号成立は、a=0またはb=0。
（証明終わり）こんな計算はしたくない。
そこで、ずるをするにゃ。 
【ずるい証明】
は増加関数。
|a|+|b|≧|a+b}だから 
（証明終わり）
問題２ 
なるとき、
と
の大小関係を調べよ。ただし、p>0、q>0、p+q=1とする。
しかし、面倒な計算はしたくないので、これから、ずるをするにゃ。
１年ほど前に、微分積分で凸関数というものをやった。凸関数は次のようなもの。
y=f(x)上の相異なる任意の２点をA(x,f(x))、B(y,f(y))とすると、この２点を結ぶ線分（弦）ABがこの曲線の弧ABよりも上にあるものを凸関数という。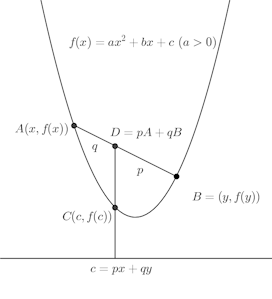
f(x)=ax²+bx+c（a>0）のときは、凸関数。で、p>0、q>0、p+q=1のとき、px+qyというのは、x軸上の(x,0)と(y,0)をq:pで分けた点と考えることができる。また、
とすると、この点は線分ABをq;pに分ける点と考えられる。Dは線分AB上にあるので、曲線上の
よりも上にある。
２次関数の図形的な意味を考えれば、計算をすることなく、大小関係を判定できるという話。
この問題の出題者は、このことを念頭にこの問題を作ったのだから、ケチをつけられる筋合いはない。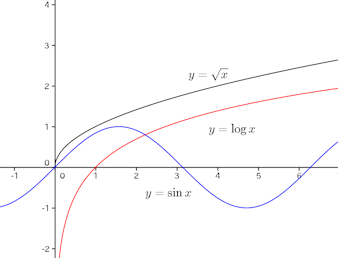
また、
p>0、q>0、p+q=1のとき
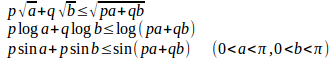
という不等式が得られる。
等号成立は、いずれの場合もa=b。さり気なく、α≧0、β≧0とし,p=1/3、q=2/3とすると
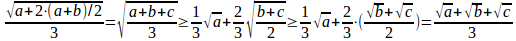
ここで、さらにもっと大胆に、a=x²、b=y²、c=z²とすると
（１） 
と
の大小を比較せよ。
（１）の不等式がどこから出てきたのかが、よく、わかる。これは関数の凸凹と深い関係があるんだケロ。
そして、
【解】
（１） x+y+z<0のとき 
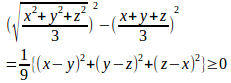
よって、
（２） （１）より
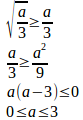
よって、a=3
また、a=3のとき①の右辺=左辺=1となり、x=y=zでなければならない。よって、x=y=z=1である。
番外編 数学的帰納法を使って、相加平均≧相乗平均≧調和平均 [ネコ騙し数学]
番外編 数学的帰納法を使って、相加平均≧相乗平均≧調和平均を！！
問題１ 次の不等式を証明せよ。ただし、文字はすべて正の数である。
相加平均≧相乗平均を使っていいというのならば、
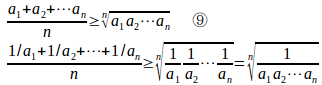
が成立するので、
しかし、大学入試でこのような証明が許されるのかといえば、駄目だろうね(^^)
だから、この問題の場合は、次のように数学的帰納法を使って証明すべきなのだろう。【証明】
（Ⅰ） n=1のとき 
（Ⅱ） n=kのとき
（Ⅲ） n=k+1のとき
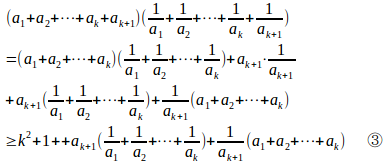
ここで、
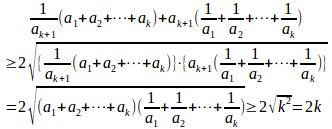
この結果を③に代入すると
数学的帰納法より、すべての自然数nについて
（証明終わり）
この不等式を使うと、
問題２ 
を正の数とする。
（１） f(x)を微分する。
とおくと、x<αではf'(x)<0、x>αでf'(x)>0なので、x=αのときf(x)は最小。
（２） n=1のとき、
だから、成立。n=kのとき
（１）の結果より、x>0ではf(x)≧f(α)
、
を上の式に代入すると、 
よって、数学的帰納法により、すべての自然数nに対して
（解答終わり）
そして、この結果を使うと、
で、問題１に戻って
番外編 さらにベクトルの問題などを [ネコ騙し数学]
番外編 さらにベクトルの問題などを
前回、次の問題を解いた。
問題４
三角形ABCの内部に点Pがある。次のことを証明せよ。（１）
（２） 点A、B、Cとは異なる点をOとする。正の数l、m、nについてのとき、△PCA:△PAB=m:n
であるとき、△PBC:△PCA:△PAB=l:m:nである。
この類題を一つ。
問題 △ABCに対して、
これは、問題４の結果を用いるとすぐに答えが出る。
②の両辺を3+4+5=12で割る。
①と③は形が違うって？
だったら、こうする。 
しかし、こんなことを知らなくても、この問題を解くことはできる。
点A、B、C、Pの位置ベクトルを
とする。
ここで閃く！！
これを使って④を書き換えると、
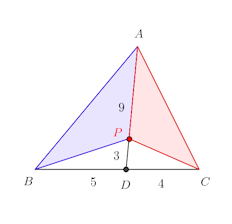
点の位置関係は図のようになり、このことから、△PCA:△PBA=4:5
であることがわかる。
また、 
△PBC:△PCA=3:4
となり、△PBC:△PCA:△PBA=3:4:5
となる。あるいは、AP:PD=9:3だから、
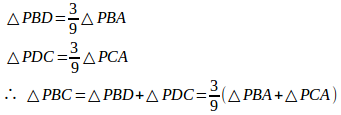
また、
「⑨ネコ、お前、何か、まだ隠し持っているんじゃないか？」
「濡れ衣だにゃ。AD:PD=(9+3):3=12:3だから、 
残りは9/12だから、
番外編 ついでだから平面ベクトルの問題を [ネコ騙し数学]
番外編 ついでだから平面ベクトルの問題を
前回の流れを受けて、平面ベクトルの問題をいくつか解いてみることにする。
問題１ 平面上に２定点A、Bがあり、その間の距離は2aである。
動点Pに対して 
（１） 点Pの動く図形を書け。
（２） 
の最大値を求めよ。
（１）
（２）
∠BAP=θとする。
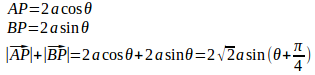
よって、θ=π/4のとき最大で、最大値は2√2a。
（解答終わり）これは、文系向けの大学入試問題なので、「三角関数の合成公式なんて習っていない」と文句がつくといけない。
cosθ+sinθの最大値をどうやって求めるか。 
x=cosθ、y=sinθとすると、
x+y=k（k>0）とすると、kの最大値は、この直線と単位円が接するときなので、
問題２ 平面上の、定点Oを始点とするベクトル
が
の終点をを頂点とする三角形はどのような三角形か。【解】
と
のなす角度は120°。同様に、と、とのなす角度も120°。したがって、この三角形は正三角形。
ベクトルの内積なんて知らないという人用のの解答は、
【別解】
より、Oは、この三角形の外心。
（別解終わり）
問題３ 平面上にO、A、Bが与えられている。このとき、次の集合を図示しろ。
（１） 境界を含む。
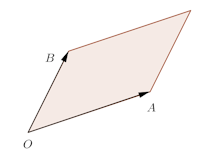
（２） 境界を含む。
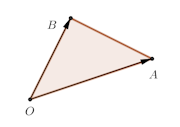
（解答終わり）
この（２）の図を頭に入れて、次の問題を解くことにする。
問題４
三角形ABCの内部に点Pがある。次のことを証明せよ。（１） のとき、△PCA:△PAB=m:n
【解】
（１） 点Pは△ABCの内部なので、0<m<1、0<n<1、0<m+n<1。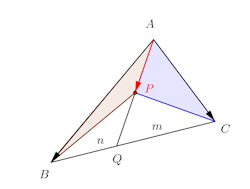
辺BCをn:mに内分する点をQとすると
したがって、
（２）
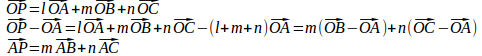
（１）より
