連続関数の性質

連続関数の性質

連続な関数には、次の性質がある。

定理１　f(x)、g(x)が区間Iで連続ならば、f(x)±g(x)、f(x)g(x)もIで連続である。また、g(x)≠0）ならば。f(x)/g(x)も連続である。

定理２　f(x)が区間Iで連続、g(x)が区間J（⊃f(I)）で連続ならば、g(f(x))はIで連続である。

定理３　f(x)が点aで連続、かつ、f(a)≠0ならば、aの十分近くの点xでは、f(x)はf(a)と同符号である。

定理４　（中間値の定理）　f(x)が閉区間[a,b]で連続、f(a)≠f(b)であるならば、f(a)とf(b)の間のすべての値γに対してf(c)=γを満たすcがa<c<bに存在する。

高校数学では、中間値の定理を次のように紹介していると思う。

定理４’　（中間値の定理）　f(x)がa≦x≦bで連続な関数、f(a)とf(b)とが異符号ならば、f(c)=0になる点cがa<c<bに存在する。

【証明】

f(a)<f(b)のとき、f(a)<γ<f(b)となる適当なγをとりg(x)=f(x)−γとすると、g(x)はa≦x≦bで連続な関数で、g(a)=f(a)−γ<0、g(b)=f(b)−γ>0となり、g(a)とg(b)は異符号。よって、定理４よりg(c)=0を満たすcがa<c<bに存在する。
f(a)>f(b)のとき、f(a)>γ>f(b)となる適当なγをとりg(x)=f(x)−γとすると、g(x)はa≦x≦bで連続な関数でg(a)=f(a)−γ>0、g(b)=f(b)−γ<0で異符号。
よって、定理４よりg(c)=0を満たすcがa<c<bに存在する。

（証明終わり）

逆に定理４’から定理４を証明することもできる。

例１　f(x)=xとし、−1≦x≦1とすると、f(−1)=−1、f(1)=1で異符号。また、f(x)=xは−1≦x≦1で連続なので、中間値の定理より、f(c)=0となるcが−1≦c≦1に存在する（c=0）。

例２　f(x)=x³−3xとし、−2≦x≦2とする。f(x)=x³−3xは−2≦x≦2で連続で、f(−2)=−2、f(2)=2と異符号。したがって、f(c)=0となるcが−2<c<2に存在する。

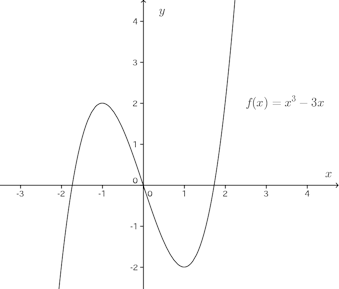
グラフから分かるように、この場合、f(c)=0となる点は一つではないことに注意（c=0、c=±√3）。
中間値の定理が保証する内容は、少なくとも一つf(c)=0となる点が存在していることを保証しているに過ぎない。

例３　f(x)=x²、−1≦x≦1のとき、f(±1)=1で同符号であるが、f(c)=0となる点cが−1<c<1に存在する（c=0）。したがって、中間値の定理を満たさなくても、a≦x≦bで連続な関数f(x)が、f(x)=0の解をもつことがある。

問　f(x)=1/xとすると、f(−1)=−1<0、f(1)=1>0であるが、−1<x<1でf(x)=0となる解を持たない。これは何故か、説明せよ。

【答】　x=0でf(x)=1/xは不連続だから。

問題１　方程式ax²−x+1=0（aは実数）が実根をもつとき、１つの実根は２より大きくない正の数となることを証明せよ。

【解】

（ⅰ）　a=0のとき、x=1。

（ⅱ）　a≠0のとき、ax²−x+1=0が実根をもつことより、この２次方程式の判別式をDとすると、

　　

である。

f(x)=ax²−x+1とすると、これは連続な関数で、

　　

f(2)=0のとき、x=2はこの方程式の解。

f(2)<0のとき、f(x)は連続な関数で、f(0)>0、f(2)<0だから、f(x)=0となる解が0<x<1に存在する。

（ⅰ）、（ⅱ）より、方程式ax²−x+1=0（aは実数）が実根をもつとき、１つの実根は２より大きくない正の数である。

（解答終わり）

問題２　g(x)は0≦x≦1で連続な関数で、0≦g(x)≦1であるとき、g(c)=cとなる点cが存在することを証明せよ。

【解】

（ⅰ）　g(0)=0のとき、c=0とすればよい。（g(0)=0、g(1)=1の場合は、c=0、c=1のどちらでもよい）

（ⅱ）　g(1)=1のとき、c=1とすればよい。（g(0)=0、g(1)=1の場合は、c=0、c=1のどちらでもよい）

（ⅲ）　0<g(0)<1かつ0<g(1)<1の場合。

f(x)=g(x)−xとすると、f(x)は0≦x≦1で連続。

さらに、

　　

であるから、中間値の定理より、0<c<1に

　　

を満たすcが存在する。

（ⅰ）、（ⅱ）、（ⅲ）より、

g(x)は0≦x≦1で連続な関数で、0≦g(x)≦1であるとき、g(c)=cとなる点cが存在する。

（解答終わり）

最後に、連続関数の最大・最小値の定理を付け加える。

定理５　f(x)が閉区間[a,b]で連続のとき、f(x)は[a,b]で最大値、最小値をとる。

例４　f(x)=xとする。このとき、f(x)は連続な関数は−1<x<1で連続な関数であるが、−1<x<1でf(x)の最大値、最小値は存在しない。

また、のとき、−2<x<2と区間が開区間であっても、最大値、最小値が存在する。x=−1のとき、最大で最大値は2、x=1のとき最小で最小値は−2である。

タグ：微分積分