ワンポイントゼミ６ 極大と極小 [ネコ騙し数学]
ワンポイントゼミ６ 極大と極小
極大、極小の定義
関数f(x)が点x=x₀においてとる値f(x₀)がx₀の近傍（x₀を含む十分小さな開区間）で、x≠x₀ならばf(x₀)>f(x)（f(x₀)<f(x)）であるとき、f(x)はx=x₀で極大（極小）といい、f(x₀)を極大値（極小値）という。極大値、極小値をあわせて極値という。
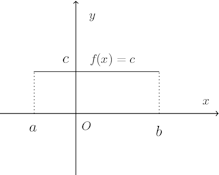
問１ 定義域をa≦x≦b（a<b)とする定数関数f(x)=cがある（cは定数）。
f(x)が極大、極小になる点とその値を求めよ。
【答】
（おしまい）
x₀≠xならばf(x₀)>f(x)=c（f(x₀)<f(x)=c）である点x₀がx₀∈[a,b]に存在しない――そのような点x₀が存在するとすれば、f(x₀)>c（f(x₀)<c）になってしまい、f(x₀)=cに矛盾する――。したがって、この場合、極大値、極小値とも存在しない。
問２ 実数全域で定義された次の関数f(x)がある。
【答】
f(x)は 
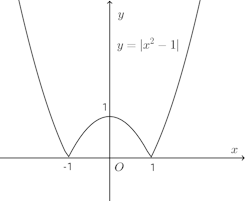
x=−1の十分に近いところにおいて、x≠−1ならばf(x)>f(−1)=0が成立するので、x=−1で極小。
x=1の十分に近いところにおいて、x=1ならばf(x)>f(1)=0が成立するので、x=1で極小。x=0の十分に近いところにおいて、f(x)<f(0)=1だから、f(x)はx=0で極大。
したがって、
極小値0 （x=±1）極大値0 （x=0）
（おしまい）関数が微分可能であるとき、極値をとる点aでは、かならず、f'(a)=0でなければならない。
問２の関数は、x=±1以外では微分可能で、その導関数f'(x)は
だからx=0でf'(0)=0となり、この条件を満たしている。
しかし、x=±1で、f(x)は微分可能でないから、この条件を満たしていない。そもそも、導関数f'(x)はx=±1で定義されていない。
また、f(x)=x³は実数全域で微分可能であるけれど、f'(x)=3x²=0となる点x=0で極値をとらない。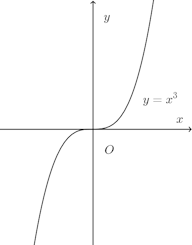
このことから、f'(a)=0という条件は、微分可能な関数f(x)がx=aで極値をもつための十分な条件でないことがわかる。f'(x)=0という条件は、微分可能な関数f(x)が極値を持つために満たさなければならない、必要な条件にすぎない！！
ひとつ質問をするが、
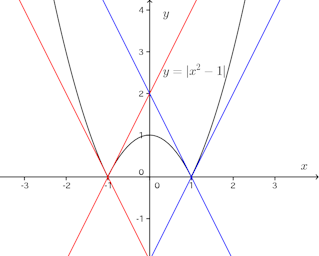
赤と青で示されている直線がこの曲線の接線？
それとも、これとは違う他の直線。
あるいは、接線は存在しない(^^)
３次方程式２ [ネコ騙し数学]
３次方程式２
問題１ ３次方程式x³+px+q=0が重複解をもつとき、
【解】
f(x)=x³+px+qとおき、３次方程式f(x)=x³+px+q=0の重複解をαとすると、 
②の微分のところでは、次の微分公式を使っている。
問題２ ３次方程式x³+px²+q=0が重複解をもつとき、pとqにはどのような関係があるか。
【解】f(x)=x³+px²+qとおき、αを重複解とすると、
よって、
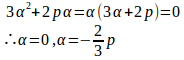
（１） α=0のとき、①よりq=0。
（２） 
のとき、これを①に代入すると
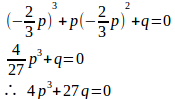
よって、
4p³+27q=0、または、q=0。（解答終わり）
ちなみに、p=q=0のときは、３重解でx=0が解。
問題３ a、b、cが相異なる実数で、
一見すると、３次方程式とは関係なさそうな問題ですが・・・。
【解】
３次方程式の解と係数の関係より、
よって、f(t)は
で極小値をとる。
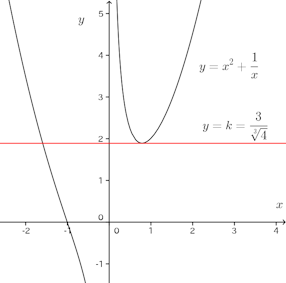
f(x)=kの実数解の個数とy=kとy=f(x)の交点の個数は等しいので、相異なる③つの実数解をもつためには
次のように、y=x³+1とy=kxとの交点の数を調べて、kの範囲を定めてもよい。。
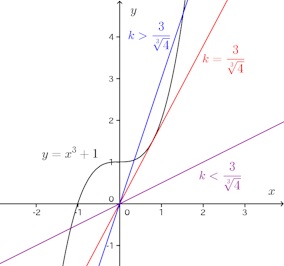
曲線y=x³+1上の点(t,t³+1)における接線の方程式は
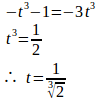
この時の傾きは
したがって、y=kxがy=x³+1とに接するとき
