第５回 余弦定理 [ネコ騙し数学]
第５回 余弦定理
余弦定理には、第１余弦定理、第２余弦定理の２つがある。そして、一般に余弦定理と呼ばれているものは、第２余弦定理だケロ。
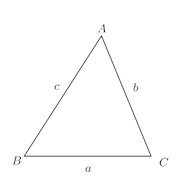
第１余弦定理
第２余弦定理
§１ 第１余弦定理
第１余弦定理を証明するにゃ。
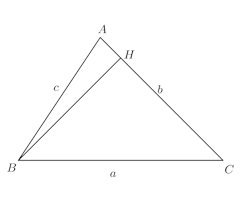
【証明】Aから線分BCに垂線をおろし、その垂線の足をHとする。
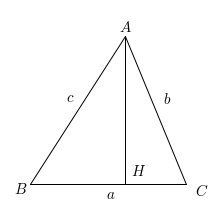
この時、
よって、
b、cについても同様。
（証明終わり）
なのですが、次のような∠Bが鈍角の鈍角三角形の場合もある。
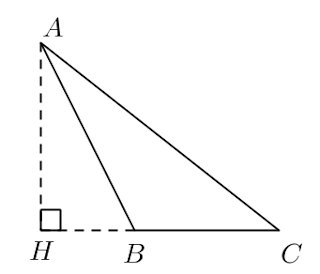
このときは、
鋭角三角形、直角三角形、鈍角三角形であろうが、いずれにせよ、成り立つというわけです。
この定理は、実は、意外に使い道がない(^^ゞ
§２ 第２余弦定理
【証明】
点Bから線分CAに垂線をおろし、その垂線の足をHとする。
△BHAは直角三角形なので、
そして、三角比より
（証明終わり）
ここでも、先の第１余弦定理の証明と同じように、鋭角、直角、鈍角三角形に分けて証明しないといけないけれど、面倒なのでしないにゃ。
その代わりに、ベクトルの内積を用いた証明を紹介するにゃ。
これは循環論法で証明になっていないという話もあるが(^^ゞ
気が向いたら、証明を付け足すにゃ。
余弦定理から三角形の三辺の長さが与えられていると、次のように角度を求めることができる。
非常に美しい式の形をしているので、この式が好きだというヒトは結構いるにゃ。
問題 △ABCにおいて、BC=4、CA=5、AB=6のとき、
（１） cosBを求めよ。
（２） sinBを求めよ。
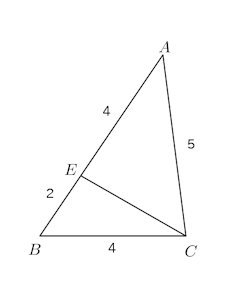
（４） 辺AB上の点EをAE=4となるようにとったとき、CEの長さを求めよ。
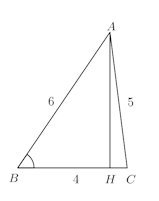
【解】
（１） a=BC==4、b=CA=5、c=AB=6とすると、余弦定理より
（２） sin²B+cos²B=1だから
（３） AH=AB×sinBだから
（４） △BCEに対して余弦定理を用いると
実は、（１）、（２）は、ヒントとなるように付け足した小問なんだけれど、余弦定理の使い方がよくわかるいい問題だと思う。
（３）、（４）は、三平方の定理と２次方程式を用いれば、余弦定理を使わなくても解けることは解けるけれど、計算が大変だケロよ。
