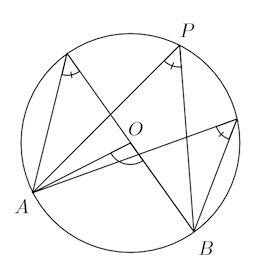
第6回 正弦定理 [ネコ騙し数学]
第6回 正弦定理
正弦定理を紹介する前に、その前提となる円周角の定理を紹介。
§0 円周角の定理
円周角とは、円周上の1点から、これとは異なる同一円周上の2点に線分を引き、この2つの線分のなす角のことである。
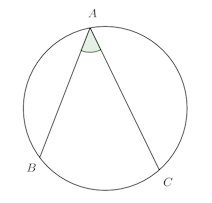
上の図の∠CABが円周角。
円周角の定理
円周角はその弧に対する円周角の半分に等しい。
この定理の証明はしない。これを前提として議論を進めることにする。
さらに、円周角の定理から出てくるのだけれど、半円の円周角は直角90°であることも前提として話を進めるにゃ。§1 正弦定理
正弦定理
△ABCの外接円の半径をRとするとき、である。
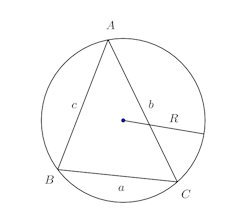
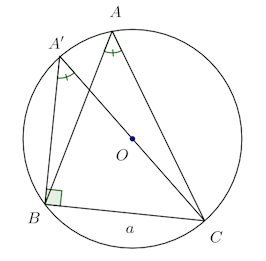
【証明】
Cと円の中心Oを通る直線と円の交点をA’とする。円周角の定理より、∠A=∠A’で、かつ、∠A'BC=∠R。
ゆえに、
同様に、各辺に対して行えば
∠Aが鋭角ならばこれで証明終わりだけれど、例によって、直角、鈍角の場合も証明しなければならない。
直角の場合は、∠A'=∠Rの時だからいいでしょう。なので、鈍角の証明をするにゃ。
弦BCに関してAとは反対側の円周上に点Dをとる。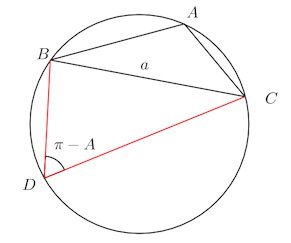
四角形ABDCは円に内接するので、
△BDCに関しては
で、三角関数の角関係を使うと
(証明終わり)
問題1 △ABCについて、次のものを求めよ。
a=10、b=10√3、A=30°のとき、cとBとCを求めよ。【解】
正弦定理より
正弦定理より
C=30°=Aになるので、c=a=10として出してもいいにゃ。
チョット先取りになるけれど、△ABCの面積Sは
問題2 △ABCにおいて、A:B:C=2:3:7、b=10のとき、△ABCの外接円の面積を求めよ。
【解】A:B:C=2:3:7より、B=45°。
外接円の半径をRとすると
何故、Bが45°になるかというと、
問題3 次の等式を満たすとき、△ABCどんな三角形か。
正弦定理より
(2) 代入すると、