三角関数の第17回の問題2の(3)を微分を使って解く [ネコ騙し数学]
三角関数の第17回の問題2の(3)を微分を使って解くと・・・
問題
第17回の問題2の(3)を、微分を使ってとこうという企画です。
この関数の最大、最小値やグラフの概形を書くために微分する。
2sinx+1=0の解は
極値の判定は、f''(x)を求めて、f'(x)=0を満たすxに対して、f''(x)<0ならば極大、f''(x)>0ならば極小を用いてもいいけれど、この場合、計算が少し面倒なので、増減表を使って極値の判定をすることにするにゃ。
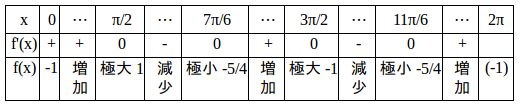
そして、
を前回と同じように
第17回 問題演習ラスト [ネコ騙し数学]
第17回 問題演習ラスト
問題1
(1) x=sinθ+cosθとおき、yをxの式であらわせ。
(2) 0<p<1のとき、yの最大値および最小値を求めよ。【解】
(1)
(2) 合成公式から、
これで、xの定義域が定まった。
そして、(1)で求めたxの2次関数を基本変形する。
このグラフの概形を書くと、x=−pのとき最小で、x=√2のときに最大になることが分かる。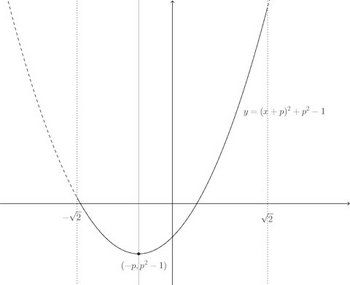
(解答終わり)
xの範囲を求めるのに三角関数の合成公式を使っているけれど、シュワルツの不等式を使うと
ちなみに、シュワルツの不等式は
問題2 関数
(1) sinx=tとおきyをxであらわし、そのグラフを書け。
(2) yの最大値、最小値を求めよ。また、そのときのxの値を求めよ。(3) xについての方程式
【解】
(1)
(2)yを基本変形する。
t=1のとき最大で、最大値は1。t=sinx=1なので、x=π/2。
(3)
このままでは調べられないので、
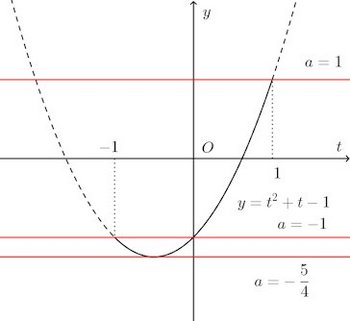
a=−5/4のとき、t=−1/2で1個。
−5/4<a≦1のとき、2個。
1<a≦1のとき1個。これでオシマイじゃじゃ〜ない。
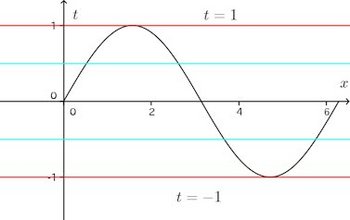
つまり、t=sinxを満たすxは、t=±1のときは1個。−1<t<1のとき2個ある。
ということで、解の個数は、
a=−5/4のとき、2個−5/4<a<−1のとき、4個
a=−1のとき、3個−1<a<1のとき、2個
a=1のとき、1個これが(2)の答えとなる。
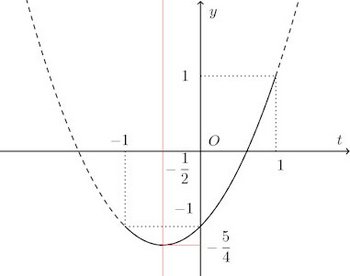
微分を使えば、次のような図を書けるけれどね〜。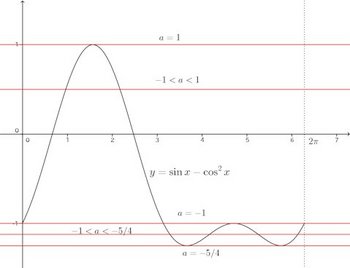
このグラフを見れば、このことがわかると思う。
もしこれを、三角関数の微分を知らない文系さん用の入試問題に出したのであれば、落とすことを目的にした大学入試の問題とは言え、(2)は「数学嫌い」や「数学アレルギー」を作るだけで、いただけない。