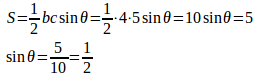第７回 三角形の面積

第７回　三角形の面積

△ABCの面積Sは

　　
である。

このことは、次の図を見てもらえるとわかると思う。

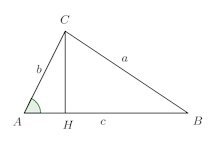
点Cから線分ABに垂線をおろし、垂線の足（交点）をHとし、△AHCに注目すれば、

　　

になるので、

　　

となるし、△CHBに注目すれば、

　　

なので、
　　

となる。

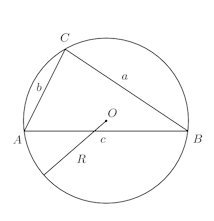
また、△ABCの外接円をRとすれば、正弦定理

　　

を使えば、三角形の三辺の長さと外接円の半径Rを使って

　　

とあらわすことができる。

△ABCに内接する円があるとする。内接円の半径をrとする。

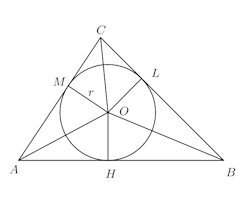
上図を見ると、△ABOの面積S₁は
　　

△BCO、△CAOの面積をS₂、S₃とすると

　　

になるので、△ABCの面積Sは

　　

になる。

つまり、三角形の面積は、三角形の三辺の長さの和と内接円の半径をかけたものを半分である

問題１　△ABCにおいて、b=4、c=5、面積5のとき、２辺b、cのなす角と辺aの長さを求めよ。

【解】

b、cのなす角度をθとすると、

　　

ここで、「わ〜い、θ=30°だ」と喜ぶと、地獄を見るにゃ。

正弦関数の角関係から

　　

が成立するので、θ=30°のとき、180°−30°=150°もこの解になる。

θ=90°の時以外は２つあるケロ。注意が必要だにゃ。

θ=30°のとき、余弦定理を使ってaの長さを求める。

　　

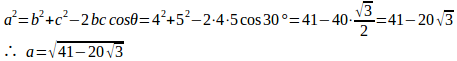
θ=150°のとき

　　

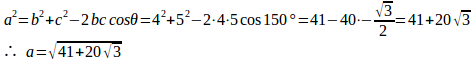
問題２　半径rに内接する正三角形の面積を求めよ。

【解】

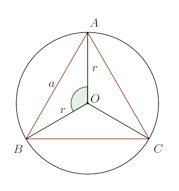
正三角形なので中心角∠AOB=120°。

よって、△AOBの面積は

　　

これを③倍したのが正三角形の面積なので、

　　

ちなみに、

　　

と簡単に求まる。

【別解】

①を使うならば、次のようにやればよい。

正三角形の一辺の長さをa、面積をSとする。

①より、

　　

また、

　　

よって、

　　

a≠0だから、両辺をa²で割っても構わないから

　　

どっち使っても同じだけれど、

　　

問題３　四辺形の対角線の長さをa、b、それとなす角をθとすれば、この四辺形の面積Sは

　　

で与えられることを証明せよ。

【解】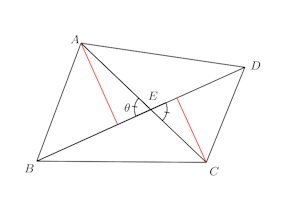

△ABEに注目する。この三角形の高さは

　　

そして、これは三角形ABDの高さでもある。

よって

　　

△AEBに注目すると、この三角形の高さは

　　

よって

　　

ゆえに、四角形の面積は

　　

a=BD、AC=bとおけば、

　　

（証明終わり）

 

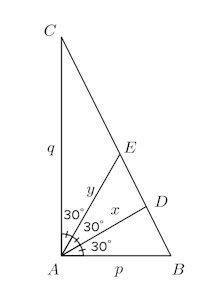
問題４　直角三角形ABCの直角Aの３等分線が斜辺BCと交わる点を、Bの方から順にD、Eとして、AB=p、AD=x、AE=y、AC=qとする。

（１）　三角形の面積を利用して

　　

が成り立つことを証明せよ。

（２）　p=1、q=2のとき、x、yの値を求めよ。

【解】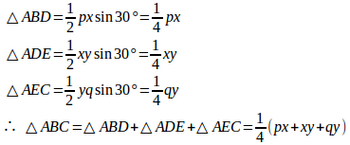

（１）

 　　

また、

　　

よって、

　　

この両辺にpqを足す。

　　

（２）　p=1、q=2だから

　　

で、
　　

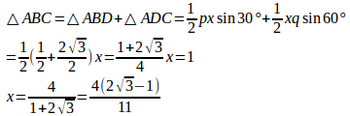
また、

　　

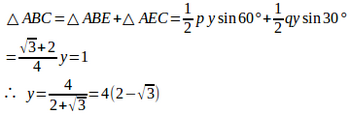
（１）の結果を使えというのかもしれないけれど、コッチのほうが楽でしょう。

タグ：三角関数