微分積分 関数の極限の計算 [ネコ騙し数学]
微分積分 関数の極限の計算
§１ 関数の極限
変数xの値がある一定の値にかぎりなく近づくことを
と書く。そして、xがaに限りなく近づくとき、関数f(x)がbに限りなく近づくことを
または
とあらわし、bをf(x)の極限値という。
次の例のようにf(a)が存在するとは限らないので注意が必要。
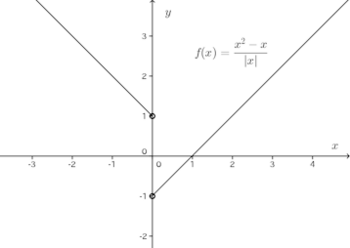
例１ 
はx=1のとき、値は存在しない。
例２ 
はx=0のとき、値は存在しない。
とあらわすと、このとき 
のx=0における右側極限という。左側からxが0に限りなく近づくことを
であらわすと、このとき
とあらわし、のx=0における左側極限という。
xがaに右側から近づくことを
、左側からaに近づくことを
であらわすと約束すると、f(x)のx=aにおける右側極限は
f(x)のx=aにおける左側極限は
そして、右側極限、左側極限と極限について、次のことが言える。
特に、a=0のとき、
を
とあらわすことがある。
§２ 問題
問題１ 次の極限を求めよ。
（１） このタイプの問題は、次のように因数分解をし、共通する因数で通分する。
（２）
（３） このタイプの極限は、次のように分子の有理化をはかってから極限を求める。
問題２ 次の関係が成り立つように、定数a、bを定めよ。
のとき、分母の
になるので、このとき、分子の
にならなければならない。
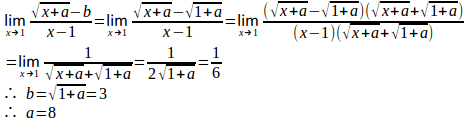
a=8、b=3のとき、この極限は1/6になるので、a=8、b=3である。
（解答終わり）
級数の収束の番外編 [ネコ騙し数学]
級数の収束の番外編
この級数の収束はどう証明したらいいんだろう？
ふっと、そんなことが頭に浮かんだ。
定理
α>1ならば 
は収束し、α≦1ならば発散する。
この定理（？）を使えば、この級数の収束の判定はすぐにできる。
しかし、こんな定理を知らなくても、
k≧2のとき、k–1≦x≦kで 
は単調増加数列で有界だから収束する。
そして、この証明は、k²やx²をαに変えれば、定理（？）の証明にそのまま流用できる。
しかし、それじゃ〜つまらない。
それで、少し――数秒――考えた。 
あるいは、k≧2のとき
この結果は、積分を使った証明と同じ結果じ。
これは、 
かつて、大学入試で次のような問題が出たことがあるらしい。
問題 
が収束する。このことを用いて
が収束することを示せ。
証明では何をどこまで使っていいのかがわからないので困ってしまうのだが・・・。
【解】
また、
平面図形と式 平面座標 [ネコ騙し数学]
平面図形と式 平面座標
平面座標を使って、重心、外心の問題を解くことにします。
その前に、平面座標の基本事項の復習。１ ２点間の距離
２点A(x₁,y₁)、B(x₂,y₂)の距離ABは 
２ 内分と外分
２点A(x₁,y₁)、B(x₂,y₂)を結ぶ線分をm:nに内分する点は 
３ 重心
３点A(x₁,y₁)、B(x₂,y₂)、C(x₃,y₃)を頂点とする△ABCの重心の座標は 
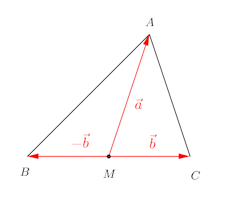
３の重心の座標の式⑤だけがあらたに出てきたので、これを導くことにする。
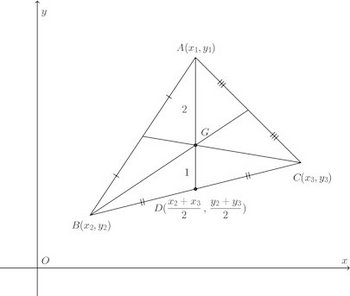
BCの中点を
とすると、Dは
では、問題を。
問題１ 平面上に２点A(−2,1)、B(3,2)がある。
（１） 線分ABを2:3に内分する点、外分する点を求めよ。（２） 点Bに関して、点Aと対称な点の座標を求めよ。
（３） ２定点A、B等距離にある点をx軸上に求めよ。【解】
（１） 内分する点Cは 
ウォーミングアップを済ませたところで、本格的な問題を。
問題２ ３点A(−5,5)、B(−2,6)、C(2,4)を頂点とする△ABCの重心Gと外心Dの座標を求めよ。
【解】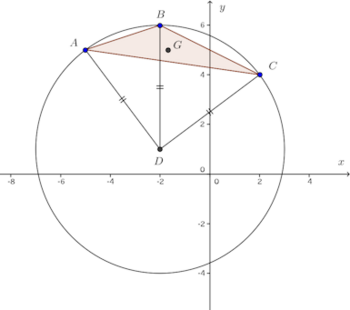
重心Gの座標を(x,y)とすると
Dは外心なのでAD=BD=CD、よってAD²=BD²=CD²。
よって、D=(−2,1)。
（解答終わり）座標を使うと、このようにして重心、外心を求めることができる。
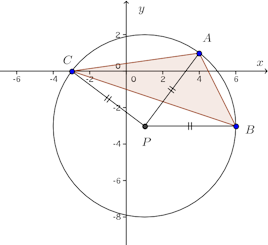
問題３ ３点A(4,1)、B(6,−3)、C(−3,0)が与えられている。
（１） A、B、Cから等距離にある点Pの座標を求めよ。（２） AQ²+BQ²が最小となるようなx軸上の点Qの座標を求めよ。
【解】（１） 点Pの座標を(x,y)とする。
よって、P(1,−3)。
（２） Q(x,0)とする。
よって、Q(5,0)。
（解答終わり）問題３の（１）の点Pは、△ABCの外心。
ベクトル 内積の不等式への応用 [ネコ騙し数学]
ベクトル 内積の不等式への応用
成分で表される２つの平面ベクトル
があるとき、その内積は 
になる。
空間ベクトルの場合、つまり、
のとき、この内積は
では、問題。
問題１ ベクトルの内積を利用して、次の不等式を証明せよ。
【証明】
とし、この２つのベクトルのなす角度をθとする。
等号が成立するのはcos²=1、または、
または
のとき。
cos²θ=1になるのはθ=0またはθ=180°のときで、これは
。
またはまたはのときである。（証明終わり）
また、
は一般に成り立つので、
とすれば、次の不等式が得られる。
これを使って、次の問題を解くことにする。
問題２ x、y、zが負でない実数でx+2y+3y=1のとき
【解】
こうした解法がいいかどうかは別にして、こういうふうに解くことができる。
次の問題は有名問題なので、やらないわけにはいかない。
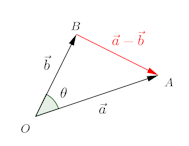
問題３ 零ベクトルでない２つのベクトル
が与えられている。
が最小となるとき
（１） tの値を求めよ。
（２） 
と
が直交することを示せ。
（１） 
だから２乗しても大小関係は変わらない。だから、を２乗する。
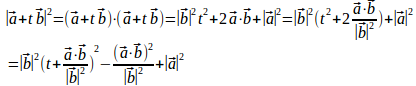
よって、
（２）
よって、とが直交する。
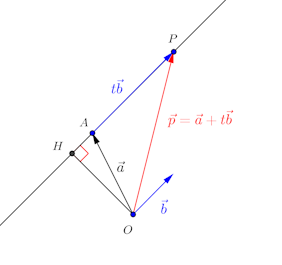
とすると、点Pは
で表される点Aを通り、に平行な直線上の点。
は、原点Oと点Pとの距離。
原点Oからこの直線におろした垂線の足をHとすると、（２）では、直線と原点との距離が最小のとき、OHと直線が直交しているということを表している。
この問題、解けるケロか？ [ネコ騙し数学]
直径１０ｃｍの円の中に、同じ大きさの正方形が５つぴったりおさまっています。この正方形１つの面積は何ｃ㎡ですか。？https://t.co/UP1IMrSYcf
— トイダス (@toidasnet) 2016年7月16日
簡単な問題なのだけれど、この記事の解法とは違う解き方で解いてみようじゃないか。
次の図のように対角線をABを引く。
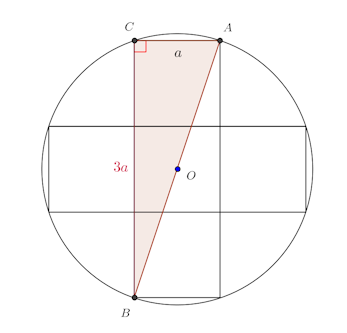
∠ACB=90°だから、ABはこの円の直径（円周角の定理）。
、小さな正方形の１辺をaとすると、AC=a、BC=3a。
△ABCは∠C=90°の直角三角形なので、三平方の定理が成り立つ。
BC²+AC²=AB²
(3a)²+a²=10²
10a²=100
∴ a²=10
小さな正方形の面積はa²だから、答えは10cm²である。
如何でしょうか？
この他にも解法は思いつけれど、これが一番自然な考えだと思うにゃ。
ベクトル 空間ベクトルの内積２ [ネコ騙し数学]
ベクトル 空間ベクトルの内積２
問題１ 空間中に３点A、B、Cが与えられている。ただし、この３点は１直線上にないものとする。原点Oからこの３点を通る平面におろした垂線の足をHとする。次の問いに答えよ。
（１） 
を証明せよ。
（２） A、B、Cの座標をそれぞれ(1,0,0)、(1,1,0)、(−1,2,1)とするとき、Hの座標を求めよ。
【解】
（１） Hは原点OからA、B、Cを通る平面におろした垂線だから、OH⊥AH。
（２） Hの座標を(x,y,z)とする。
よって、
うるさいことを言うと、求めたH(1/5,0,2/5)がA(1,0,0)、B(1,1,0)、C(−1,2,1)と同一平面にあることを示さないといけない。
A、B、Cの３点を通る平面の方程式を 
しかし、ここまでするのであれば、次のように解答したほうがいい。
垂線OHは(1,0,2)に平行（※）。
点Hは垂線(x,y,z)=(t,0,2t)と平面x+2z=1の交点。よって、
このように解答すれば、連立２次方程式を解かなくてすむし、面倒な議論をしなくてすむ。
（※） 平面π：ax+by+cz=dと
は垂直！！
平面π上に(x,y,z)とは異なる点
があるとすると
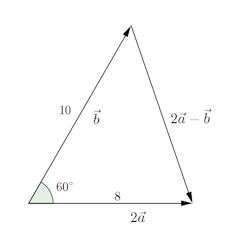
は垂直。問題２ Oを座標の原点とし、
（１） ∠ABC=θとして、cosθを求めよ。
（２） △ABCの面積を求めよ。【解答】
（１） 
（２） cosθ=1/2よりθ=60°。
ベクトル 空間ベクトルの内積と成分 [ネコ騙し数学]
ベクトル 空間ベクトルの内積と成分
§ 空間ベクトルの内積の成分表示
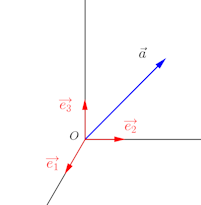
空間では、ベクトル
は次のように３つの成分で表される。
基本ベクトル
を用いて表すと
したがって、との内積は
となり、
何故ならば、
だから。
§ 方向余弦
x軸、y軸、z軸の正の向きとベクトルのなす角を、それぞれ、α、β、γとすると
また、
この３つの組をの方向余弦といい、
のとき
したがって、方向余弦には次の関係がある。
§ 問題編
ベクトルのなす角θ
問題１ 
のなす角θ（0°≦θ≦180°）を求めよ。
（解答終わり）
問題２ 
のとき
（１） ベクトルのなす角を求めよ。
（２） の両方に垂直な単位ベクトルを求めよ。
（１） 
、また
（２） の両方に垂直な単位ベクトルを
とする。
はに垂直なので 
問題３ 大きさが２、x軸、y軸の正の向きとなす角がそれぞれ45°、60°であるベクトルの成分を求めよ。、また、そのベクトルがz軸の正の向きとなす角度を求めよ。
【解】求めるベクトルの方向余弦をl、m、nとすると
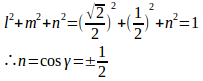
したがって、γ=60°、120°。
求めるべきベクトルをとすると
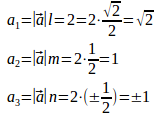
よって、(√2,1,1)または(√2,1,−1)。
（解答終わり）問題３から分かるように、一般にベクトルがx軸、y軸、z軸の生の向きとなす角α、β、γの和α+β+γは、一般に180°にならないので、注意して欲しいにゃ。
ベクトル 内積と成分（平面の場合） [ネコ騙し数学]
ベクトル 内積と成分（平面の場合）
平面上にある２つのベクトルの内積
の成分表示を求めることにする。
平面上ではベクトルの成分は
とすると、それぞれ 
したがって、内積は
また基本ベクトルは大きさが１で互いに直交するので、
と基本ベクトル
との内積は
つまり、ベクトルの成分はベクトルと基本ベクトルとの内積になっている。
問題１ 
のなす角θ（0≦θ≦180°）を求めよ。
内積の定義は
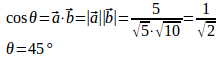
問題２ ベクトル
に垂直で、大きさが
に等しいベクトルを求めよ。
とする。
だから
だから
よって
問題３ ３点A(−1,0)、B(0,2)、C(−3,1)が与えられている。
を満たす第１象限の点Dの座標を求めよ。
点Dの座標を(x,y)とする。
Dは第１象限の点なので、D(2,1)。
問題４ ベクトル
に対して、ベクトル
の成分を、次のそれぞれの場合について求めよ。
（１） とが平行の場合
（２） とが垂直の場合
（１） とが平行なので
を満たす実数kが存在しなければならない。
であり、b=−2（２） 
だから
でなければならない。
のとき 
ベクトル ベクトルのなす角とベクトルの垂直 [ネコ騙し数学]
ベクトル ベクトルのなす角とベクトルの垂直
ベクトルのなす角をθとする。
であるとき、
また、の必要十分な条件は、のとき、
、つまり
である。
問題１ △ABCと点Oについて、次のことを証明せよ。
OA⊥BC、OB⊥CAならばOC⊥ABである。【証明】
とする。
OA⊥BCから
OB⊥CAから
①と②より
よって、OC⊥ABである。
（証明終わり）これは、「三角形ABCの３垂線は一点（垂心）で交わる」ことの証明になっている。
問題２ ２つのベクトルの大きさが等しいとき、ベクトル
と
は垂直であることを示せ。
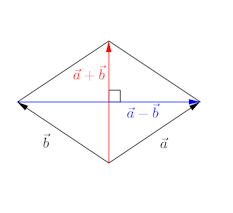
条件より
との内積をとると
よって、とは垂直である。
これは、ひし形の対角線は互いに直交することの証明になっている。
問題３ はともに零ベクトルではなく、
このとき、次の問いに答えよ。
（１）のなす角度を求めよ。（２） 
は
の何倍か。
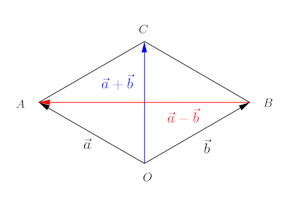
とする。
（１）
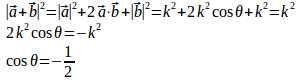
よって、θ=120°。
（２）
よって、√3倍である。
（解答終わり】
とすると、
という条件から、△OAC、△OBCは正三角形になる。
何故ならば、ベクトルの和の定義よOB=OAで、OA=AC=OBとなって、△OACは正三角形。同様に、△OBCも正三角形。
∠AOB=∠AOC+∠COB=60°+60°=120°
また、 
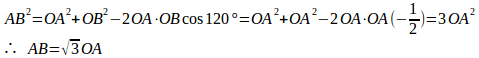
このように解くこともできる。
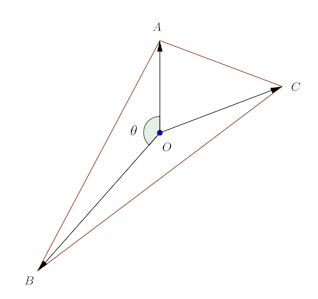
問題４ 平面上に和が零ベクトルになる３つのベクトル
があって、OA=1、OB=2、OC=√2である。
（１） 
のなす角度をθ（0≦θ≦π）とするとき、sinθを求めよ。
（３） △ABCの面積を求めよ。
（１） とする。
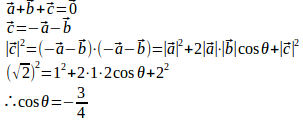
sin²θ+cos²θ=1だから
（２）
（３） 
だから、Oは△ABCの重心（※）。
（※）△ABCの重心をGとすると
△ABC=3△OABになるのは、COの延長とABの交点をDとすると、Oは△ABCの重心でCD=3ODとなるから。
ベクトル 内積の計算例 [ネコ騙し数学]
ベクトル 内積の計算例
内積の定義式は
問題１ ベクトルの内積について、次のことを証明せよ。
（１） 内積の演算規則に従って計算するならば、次のようになる。
（２） 
と考えて
（３）
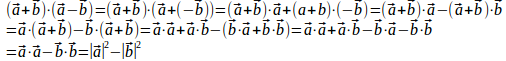
（証明終わり）
どの規則がどこで使われているかわかるように書いたけれど、実際計算するときには、このように計算する必要はない。
実数の展開の公式 
次に、（２）の計算の幾何学的な意味を考えることにする。
△OABがあり、
とすると、
そして、余弦定理から
問題２ ベクトルについて、次の等式を証明せよ。
【解】
（解答終わり）
問題１の（１）、（２）の結果を使わずに、
問題３ ベクトルの大きさがそれぞれ4、10で、のなす角が60°であるとき、
の大きさを求めよ。
【別解】
余弦定理より
