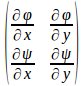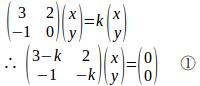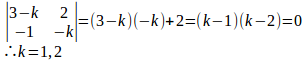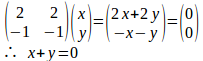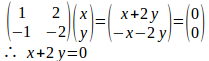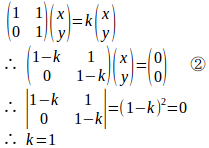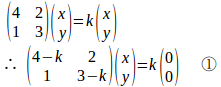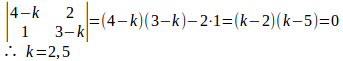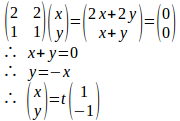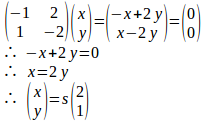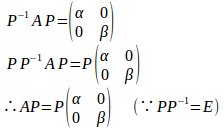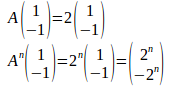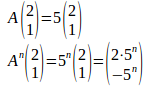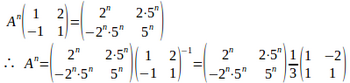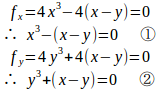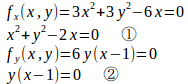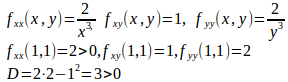第１６回 ヤコビアン [ネコ騙し数学]
第１６回 ヤコビアン
u=φ(x,y)、v=ψ(x,y)がC¹級であるとき、
をヤコビ行列といい、次の行列式
をヤコビアンという。
問題１ 次のヤコビアン
を求めよ。
【解】
（１） 
だから
（２） 
だから
（３） 
だから
（解答終）
問題２
（１） 
、
のとき、
が成り立つことを示せ。
（２） が逆に解けて、
であるとき、
であることを示せ。
（３） 平面座標の座標変換
のヤコビアン
と
を求めよ。
【解】
（１） 合成関数の微分公式（連鎖律）から
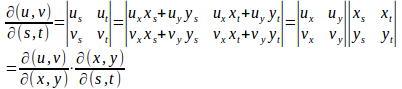
（２） （１）でs=u、t=vになっている場合だから
（３） 
だから、
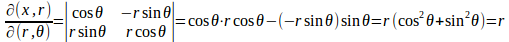
（２）より
（解答終）
問題２の（３）は
を逆に
と解くことができ、
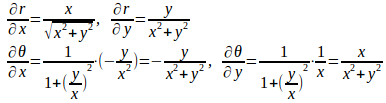
となるので、直接
と解くこともできる。
問題３ 
をC¹級の写像とする。
fがC¹級の逆写像
をもつとき、
であることを示し、これより
であることを証明せよ。
【解】
をu、vで偏微分すると、
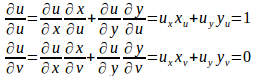
同様に、
をu、vで偏微分すると、
したがって、
よって、
（解答終）
偏微分の簡単なドリル [ネコ騙し数学]
最近、２次曲線を取り上げ、肝心の偏微分の記事をブログにアップしていない。
そこで、お前らに一つ尋ねるけれど、次の偏微分くらいは簡単に求められるんだろうな。
問題 次の関数を偏微分しなさい。
次の定理を使うと、比較的簡単に上の関数の偏微分を求めることができる。
定理 関数f(u)が微分可能で、u=φ(x,y)が偏微分可能ならば、
である。
ただ、この定理を使って実際に計算する場合は、公式（A)よりも、z=f(u)とおき、
を使ったほうが間違いにくいのだろう。
（１）の場合は、z=f(u)=√u、u=x²+y²とすると、
だから、
になる。
（２）の場合、
とおけば、
だから、
になる。
なお、
２次曲線の離心率 [ネコ騙し数学]
２次曲線の離心率
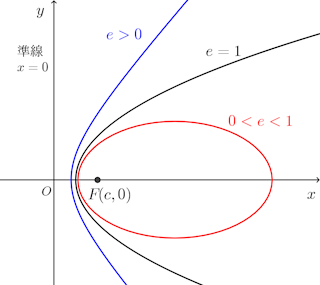
放物線の定義は、「直線（準線）と直線上にない定点（焦点）との距離が等しい点の軌跡」であり、これは「準線からの距離と焦点からの距離の比が１：１である点の軌跡」と言い換えることができる。
そこで、これをさらに一般化し、
「準線からの距離と焦点からの距離の比が１：eである点の軌跡」
について考えることにする。
準線をy軸とし、焦点Fの座標を(c,0)とすると、点P(x,y)と準線との距離は｜x｜、焦点Fと点Pとの距離は
になるので、
この両辺を２乗すると、
e=1のときは
e≠1のとき
0<e<1のとき、e²–1<0だから
e>1のとき
したがって、
0<e<1のとき楕円、e=1のとき放物線、e>1のとき双曲線である。
このeを離心率という。
楕円、双曲線の中心が原点に一致するよう、x軸方向に
平行移動すると、（３）式は
したがって、楕円
の離心率eは、
から
と求められる。
また、このとき、（４）式は
となるので、双曲線の離心率eは
から
と求められる。
２次曲線の極座標表示 [ネコ騙し数学]
２次曲線の極座標表示
§１ 楕円
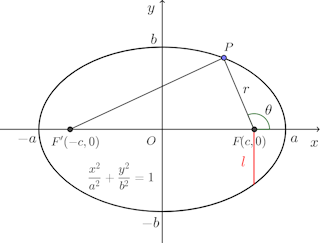楕円の焦点をF(c,0)、F'(−c,0)とし、楕円上の動点をP、FP+F'P=2aとする。
FP=r、x軸とFPのなす角度をθとする。
△FF'Pに対して余弦定理を用いると
a≠0だから、右辺の分母、分子をaで割ると、
ここで、
とおくと、楕円の極座標表示の方程式（※）は
半直弦とは、θ=π/2のときのFP=rのこと。
このことは、θ=π/2のときcosθ=0になるので、（１）式より
となることより明らかだろう。
また、楕円（a≧b）の場合、
離心率εは
である。
a=bのときは円でε=1である。
（※） この場合
という対応関係にあることに注意！！
§２ 双曲線
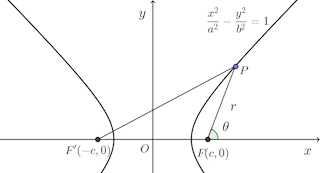双曲線の焦点をF(c,0)、F'(−c,0)とし、右側の双曲線について考えることにする。
双曲線上の点をPとすると、双曲線の定義から
FPとx軸のなす角度をθとし、△FF'Pについて余弦定理を用いると、
FP=rとすると、
ここで、aで右辺の分子分母を割ると、
ここで、
とおくと、
c>aだから双曲線の離心率ε>1である。
§３ 放物線
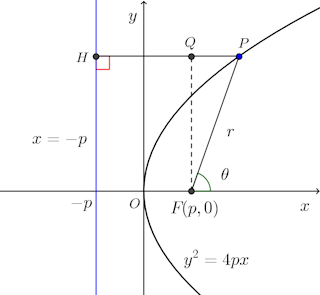放物線の焦点F(p,0)（p>0)、準線をx=−p、さらに放物線上の点をPとし、準線x=−pにPからおろした垂線の足をHとする。
放物線の定義からHP=FP。
FP=r、線分FPとx軸のなす角度をθとすると、
l=2p、ε=1とすれば、
の形になるので、放物線の離心率ε=1。
ということで、２次曲線は
0≦ε<1のとき楕円（ε=0のとき円）
ε=1のとき放物線
ε>1のとき双曲線
になるという話でした。
２次曲線 [ネコ騙し数学]
２次曲線
§１ 楕円
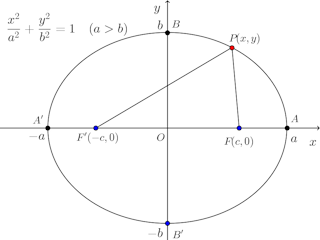
２つの定点からの距離の和が一定である動点の軌跡を楕円という。この２つの定点を楕円の焦点という。
焦点をF(c,0)、F'(−c,0)、動点Pの座標を(x,y)とし、距離の和を2a（a>c>0）とすると、
両辺を２乗すると、
両辺を２乗すると、
a²–c²=b²とおくと、楕円の方程式は
また、このことから、楕円
の焦点の座標は
AA'=2aを長軸の長さ、長径、BB'=2bを短軸の長さ、短径という。
例 楕円
a=5、b=4とすると、
よって、焦点は(−3,0)、(3,0)。
a=b>0とすると、（１）は
これは原点Oを中心とする半径aの円になる。そして、このとき、焦点は円の中心Oになる。
§２ 双曲線
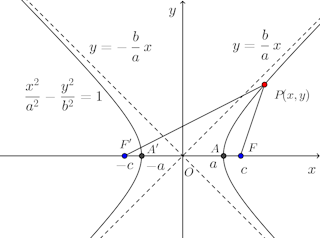
２定点からの距離の差が一定である動点の軌跡を双曲線という。
この２定点を双曲線の焦点という。
２定点をF(c,0)、F'(−c,0)、動点Pの座標を(x,y)、距離の差を2a(c>a)とする。
両辺を２乗すると、
両辺を２乗すると、
c²–a²=b²とおくと、
双曲線
の焦点は
である。
双曲線の漸近線は、
§３ 放物線
定点と定直線との距離が一定の動点の軌跡を放物線という。
このとき、定点を放物線の焦点、定直線を準線という。
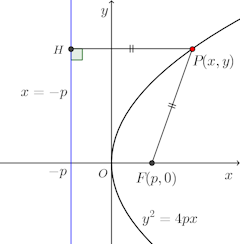定点Fの座標を(p,0)、定直線（準線）をx=–p、動点Pの座標を(x,y)とし、Pから直線x=–pにおろした垂線の足をHとする。
両辺を２乗すると、
２次曲線の標準化の例 [ネコ騙し数学]
２次曲線の標準化の例
２次曲線の方程式の一般形は
３×３の対称行列を用いると、
となる。
なのだが、座標軸の回転に関係する部分は、（１）の２次の項（の係数）だけなので、それに対応する対称行列
について、まず考える。
問題１ 次の２次曲線を標準形にせよ。
【解】
とすると、固有方程式は
t=2のとき、
t=8のとき
だから、大きさが１の固有ベクトルは、
これは、基本ベクトル
を反時計回りにθ=45°=π/4(rad)回転させたものだから、
これをに代入すると、
ここで、さらに
と座標変換すると、
よって、この曲線は楕円である。
（解答終）
これは図形や点を原点まわりに４５°回転させるのではなく、x軸、y軸を45°回転し、それを新しいx'軸、y'軸とする主軸変換、座標変換！！
そのため、
となっている。
①式は
と書き換えられるので、高校で習う１次変換とは違うことに注意！！
これ以上余計なことを書くと混乱させるだけだから、これ以上は書くまい。
問題２ 次の２次曲線を標準化せよ。
【解】
とおくと、
よって、行列Aの固有値はt=0,2。
t=2のとき
t=0のとき
したがって、行列Aの大きさ１の固有ベクトルは、
これは基本ベクトル
を４５°時計回りに回展させたものだから、
とし、x²–2xy+y²+2x–6 y=0に代入すると、
さらに、
と変換すると、
となり、この曲線は放物線である。
（解答終）
２次形式の標準化 [ネコ騙し数学]
２次形式の標準化
２次形式
変数x、yと実係数a、b、hで定められる関係式
を２次形式という。
これは行列を使うと
で表される。
列ベクトル
を転置した行ベクトル
、さらに対称行列
とすると、
例
ところで、対称行列は適当な直交行列P（
）を用いて
と対角化することができる。
そこで、
とすると、
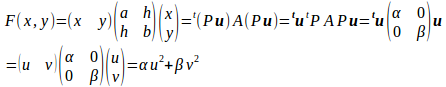
と、２次形式F(x,y)=ax²+2hxy+by²を２次形式の標準形
にすることができる。
ここで、α、βは行列Aの固有値である。
問題１ 次の２次系式を標準化せよ。
【解】
（１） 
の固有方程式は
よって、行列Aの固有値はt=2、８。
t=2のとき
t=8のとき
したがって、t=2、8のときの固有ベクトルは、
したがって、この固有ベクトルの単位ベクトルは
よって、
で、
したがって、
とすると、
（２） 
の固有方程式は
t=3に対する単位固有ベクトルは
t=−2に対する単位固有ベクトルは
したがって、直交行列Pは
となり、
したがって、
とおくと、
（解答終）
x軸とy軸をθだけ回転した新しい座標軸をu、vとする。
このとき、xy座標系での点Pの成分(x,y)と、新しいuv座標系での点Pの成分(u,v)との間には
という関係がある。
行列を用いて表すと、
ここで、
とおくと、行列Pの行と列の成分を入れ替えた行列（転置行列）
は
となり、
したがって、は直交行列。
⑨を２次形式F(x,y)=ax²+2hxy+by²に代入すると、
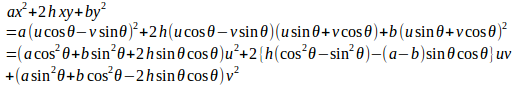
uvの項の係数を0にするには、θを
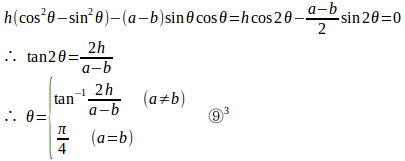
にとればよく、このようなθをとれば２次形式の標準形になる。
問題２ ２次曲線2x²–2xy+2y²=9 を標準形にせよ。
【答】
だから、
の対角化を図る。
行列Aの固有方程式は
t=1のときの固有ベクトルは
t=3のときの固有ベクトルは
固有ベクトルの正規化――大きさ１の単位ベクトルにすること――をすると、
したがって、
このようにPを選ぶと
なるケロ（実際に計算して、こうなることを確かめよ）。
だから、
として、2x²–2xy+2y²=9を標準化すると、u²+3v²=9になる。
（解答終）
行列の固有値と固有ベクトル [ネコ騙し数学]
行列の固有値と固有ベクトル
１次変換（行列）
に対して
を満たすλをAの固有値、
を固有ベクトルという。
単位行列
とすると、（１）式は
と変形できるので、
が存在するための必要十分条件は、行列A–λ Eが逆行列を持たないこと、すなわち、
で、（２）式をAの固有方程式という。
２次方程式（２）の解をα、βとすると、解と係数の関係より、
が成り立つ。
ここで、
のことで、これは行列
の行列式である。
問題１ 次の行列の固有値と固有ベクトルを求めよ。
【解】
固有ベクトルを
、固有値をkとする。
（１）
x=y=0以外の解をもつためには、
k=1のとき、①式より
ここで、x=tとおくと、y=−t。
よって、固有ベクトルは
k=2のとき①より
y=sとおくと、x=−2s。
よって、固有ベクトルは
（２）
②式より
よって、固有ベクトルは
である。
（解答終）
問題２ 次の問に答えよ。
（１） 行列
の固有値と固有ベクトルを求めなさい。
（２） 
となる行列Pを求めよ。
（３） nが自然数のとき
を求めよ。
【解】
（１） Aの固有値をk、固有ベクトルをとすると、
以外の解をもつためには、
k=2のとき、①式より
k=5のとき、①式より
（２）
ここで、
とおくと、
したがって、α、βは行列Aの固有値で、
はその固有ベクトル。
よって、α=2、β=5とすると、
（３） a=1,b=1とおく。
α=2のとき
β=5のとき
よって、
後の計算はヨロシク！！
（解答終）
が成立するので、これを利用して
と計算してもよい。
２次曲線プチ [ネコ騙し数学]
２次曲線プチ
問題１ 次の曲線を原点の周りに４５°回転してえられる曲線の方程式を求めよ。
【解】
(x,y)を原点まわりに角度θ回転して得られる点を(x',y')とすると、次の関係が成立する。
逆に、(x',y')を原点まわりに角度−θ回転すれば(x,y)に戻るので、次の関係が成立する。
したがって、θ=45°のとき、
になる。
（１） x²–y²=a²に
を代入すると、
（２） x²+xy+y²=6にを代入すると、
だから、
（３） x²–2xy+y²–2x–2y+1=0にを代入すると、
よって、
（解答終）
図形を回転させても図形の形は変わらないので、（１）のx²–y²=a²（a>0）は直角双曲線であり、（２）のx²+xy+y²=6は楕円。そして、（３）の曲線x²–2xy+y²–2x–2y+1=0は放物線である。
実は、２次曲線
には、曲線の種類を判別できる、判別式D=ac–b²という判別式があり、
D>0のとき楕円
D=0のとき放物線
D<0のとき双曲線
になる。
こうなっていることを、問題の（１）、（２）、（３）の場合で確かめて欲しいにゃ。
問題２ 曲線(x+y)²=4xとx軸で囲まれた部分の面積を求めよ。
【解】
(x+y)²=4xだから
y≧0の部分は、y=2√x–xだから、
（解答終）
問題２を解くのに２次曲線の知識は必要としないけれど、
となるので、a=b=c=1となり、２次曲線の判別式を使うと、
となり、この曲線が放物線であることが分かる。
このことは、この曲線を原点まわりに−45°回転すると、変換式は
となるので、これを(x+y)²=4x代入すると、
第１５回 ２変数関数の極値の計算例 [ネコ騙し数学]
第１５回 ２変数関数の極値の計算例
偏微分を用いて２変数関数の極値を求める前に、極値に関する定理を再掲する。
定理１５
関数f(x,y)が偏微分可能なとき、点(a,b)で極値を取るならば
である。
定理１６ （極値の判別式）
f(x,y)は領域DでC²級の関数とする。(a,b)をf(x,y)の停留点とし
とおくとき、次のことが成り立つ。
（ⅰ） D>0のとき
ならば、f(x,y)は点(a,b)で極小、
ならば、f(x,y)は点(a,b)で極大となる。
（ⅱ） D<0のとき、f(x,y)は点(a,b)で極大でも極小でもない。
（ⅲ） D=0のとき、２階の偏微分係数だけからは判定できない。
なお、定理１６に登場する停留点とは、である点を停留点のことである。
問題 次の関数の極値を求めよ。
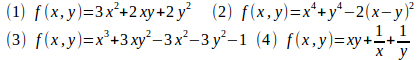
【解】
（１） 
より、停留点は(0,0)である。
だから
。
したがって、f(x,y)は(0,0)で極小で、f(0,0)=(0,0)が極小値である。
（２）
①と②を加えると
y=−xを①に代入すると、
よって、停留点は(0,0)、(√2,−√2)、(−√2,√2)である。
(x,y)=(√2,−√2)、(−√2,√2)のとき
だから
となるので極小、極小値は−8。
(0,0)のとき、D=0となり、２階偏微分係数を用いた極値の判定は出来ない。
したがって、(0,0)は極値ではない。
（３） 
したがって、停留点は
②よりy=0、x=1。
y=0を①に代入すると、x²–2x=x(x–2 )=0より、x=0、2。
x=1を①に代入すると、y²–1=(y+1)(y–1)=0よりy=±１。
よって、停留点は(0,0)、(2,0)、(1,1),(1,−1)。
よって、(0,0)のとき、
だから
となり、f(x,y)は(0,0)で極大、極大値はf(0,0)=−1になる。
(2,0)のとき、
だから、f(x,y)は(2,0)で極小、極小値はf(2,0)=−5。
(1,1)、(1,−1)のとき、
だから、極値ではない。
（４）
したがって、
②より
これを①に代入すると、
②にy=1を代入すると、x=1。
したがって、停留点は(1,1)。
よって、f(x,y)は点(1,1)で極小で、極小値はf(1,1)=3である。
（解答終）
