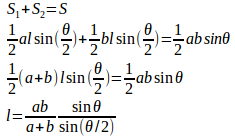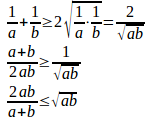番外編 循環小数の続き [ネコ騙し数学]
番外編 循環小数
循環小数については数列と級数の第19回で少しだけ触れておいただけなので、その続編です。
たとえば、0.333・・・という循環小数があるとする。
これは実は
aを1≦a≦9の自然数とする。
そして、
この極限値は簡単に求められて、
ここでは、
ということで、最初の例として出した0.3・・・は、a=3のときなので
そして、
もっとも、こんな難しい計算をしなくても、
で、もっと拡張して、
これは、
だから、たとえば、0.517517517・・・という循環少数は
ちなみに、a₁a₂a₃は数の並びで、a₁とa₂、a₃の掛け算ではないので、この点は注意してほしいニャ。
では、問題。
問題1 次の連立方程式を解け。
【解】
問題2
a、b、cは1<a<b<c<9となる整数で、
(1) a、b、cの値を求めよ。
(2) この等比数列の第四項を循環小数であらわせ。
【解】
(1)
(2)
ちなみに、(1)α、β、γが等比数列であるとき、公比をrとすると、
中学数学の復習 第1回 一次方程式 [ネコ騙し数学]
中学数学の復習 第1回 一次方程式
正と負の数の四則演算、ならびに、交換法則、結合法則、分配法則、すなわち
さらに、
a=bのとき
一次方程式(1変数の場合)
一次方程式の一般形は
だけど、何故、こう計算できるかにというと、上の結合法則や(1)〜(3)などが必要なんだケロ。
ax+b=0の両辺に−bを足す(bで引く)と、(1)より
実は、これでもまだ手抜きしているんだけれど、結構、面倒くさいことをやっているんだにゃ。
移項
等式の一方の辺にある項を、符号を変えて他方の辺に移すこと。
例
問題1 次の方程式を解け。
これまで「ねこ騙し数学」の中で解いた問題の中で一番難しい問題のように思うのは、気のせいだろうか・・・。
問題2 10%の食塩水と30%の食塩水を混ぜて、15%の食塩水を300g作るとき、10%の食塩水は何gいるか。
【解】
必要な10%の食塩水をxgとする。すると、30%の食塩水は(300−x)gとなる。
で、10%の食塩水xgに溶けている食塩の量は
こんな問題、中学校を卒業してから解いたことがないから、解いていてなんか頭がおかしくなりそうだケロ。
中学校の先生や塾の先生は、よく、こんなことを子供に教えられるよな。オレだったら、間違いなく、教えている途中で、プッツン切れしまう。平常心を保つために、大昔、大学入試などによく出る簡単な軌跡の問題を一つ解くことにするにゃ。
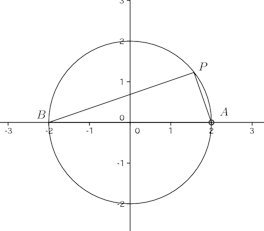
問題3 2直線
①は定点(2,0)、②は定点(−2,0)をそれぞれ通る。また、①と②の傾きはそれぞれ−k、で
よって、交点Pは2定点A、Bを直径とする円周(x²+y²=4)上に存在する。
ただし、(2,0)は除く。
何故、(2,0)がダメなのか、わかるケロか?
②式に(x,y)=(2,0)に代入すると、
また、2直線、y=mx+nとy=m'x+n'が直交する条件は
【別解】
①より
番外編 お絵描きの練習3 [ネコ騙し数学]
番外編 お絵描きの練習3
問題1 直径ABの半円がある。この半円に図のように台形ABQPを内接させるとき、その台形の面積の最大値を求めよ。ただし、AB=2rとする。
直径ABの中点をOとし、次の図のように座標平面上に台形ABQPの各点をとることにする。台形の面積をSとすると、
xとyには
――展開すると、因数分解の計算が面倒くさくなる――
いやいや、①のまま微分したほうが楽かもしれない。
問題2 半径rの円Oの周上に定点Aと動点Pがある。Aにおける円Oの接線にPからおろした垂線の足をQとする。PがAに近づくときの極限値はそれぞれどうなるか。
∠AOP=θとする。このとき、
よって、
上の計算では、
を使っているにゃ。
第7回 番外編 お絵描きの練習2 [ネコ騙し数学]
第7回 番外編 お絵描きの練習2
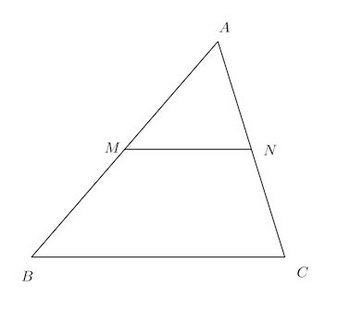
中点連結定理
三角形ABCの辺AB、ACの中点をそれぞれM、Nとするとき、である。
証明は、ベクトルを使うと、次のようになるにゃ。
【証明】
ちなみに、三角形AMNと三角形ABCは相似で相似比は1/2である。だから、面積は
ここまではイントロ。
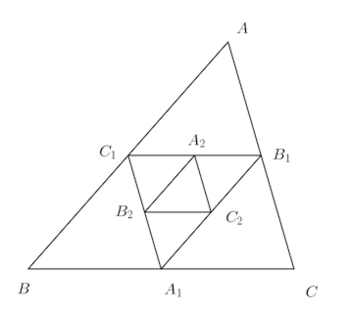
では、問題を解いてみることにするにゃ。問題
図のように△ABCの確変の中点を結び、△A₁B₁C₁をつくり、次々にこの操作を行って△A₂B₂C₂、△A₃B₃C₃、……を作るとき、その面積をS₁、S₂、S₃、……とすれば、
(1) △ABCの面積がSのとき、無限級数
(2) △ABCの週をl、△A₁B₁C₁の周をl₁、△A₂B₂C₂の周をl₂、……とするとき、
(1) △A₁B₁C₁の面積は△ABCの1/4だから
(2) △A₁B₁C₁は辺の長さがそれぞれ△ABCの各辺の長さの半分になっているのだから、△ABCとの周の長さには
よって、
ここでは、等比数列の無限級数の公式
を使っている。(1)のときa=S/4、r=1/4で、(2)のときa=l/2、r=1/2。
番外編 お絵描きの練習 [ネコ騙し数学]
番外編 お絵描きの練習
次の図に示す三角形があるとする。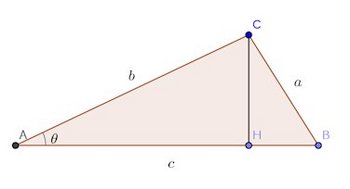
三角形の面積Sは、(底辺×高さ)÷2だから、
そして、CHは三角関数を使うと
だから、
三角形ABCがあるとする。そして、∠Aの二等分線と辺BCの交点をDとし、∠A=θとする。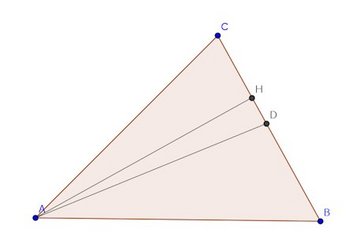
このとき、三角形ABDの面積S₁は
となり、三角形ADCの面積S₂は
だから、三角形ABDと三角形ADCの面積の比は
また、Aから辺BCに垂線をおろし、その交点をHとすると、S₁とS₂は
つまり、∠Aの二等分線は、辺BCをABとACの線分比に分ける。
この重要な性質を知っていたケロか?
三角関数を使わない証明の仕方もあるのだけれど、その証明は初等幾何をやる時に取っておくことにするにゃ。
でも、やりたいのは、これではないんだ。
問題 三角形ABCにおいて、AB=a、AC=b、∠ABC=θ、∠BACの二等分線の三角形内にある部分ADの長さをlとする。
(1) 三角形ABDの面積をa、lとθで表わせ。
(2) lをa、bとθとで表わせ。
(3) a、bを一定に保ち、θを0に近づけるとき、を求めよ。
(1)
(2)
三角形ABCの面積Sは
であり、
ここでやめてもいいのだけれど、
になるので、
としたほうが(3)の極限の計算が楽になる。
(3)
![]()
なお、ここでは三角関数の極限の基本式
そして、ここに出てくる
a>0、b>0のとき、
だから、
つまり、
となる。
相加平均≧相加平均≧調和平均
というわけでにゃ。証明は、
とやってもいいにゃ。番外編 微分積分の問題を解く5 [ネコ騙し数学]
番外編 微分積分の問題を解く5
問題1 とする。
(2) 横軸にa、縦軸にm(a)とし、このグラフをかけ。
【解】(1)
a>0のとき、
x | … | loga | … |
f'(x) | − | 0 | + |
f(x) | 減少 | 極小 a−aloga | 増加 |
よって、a>0でm(a)=a−alogaになる。
(2)
よって、0<a<1で増加、a>1で減少となり、a=1のときm(a)は極大。
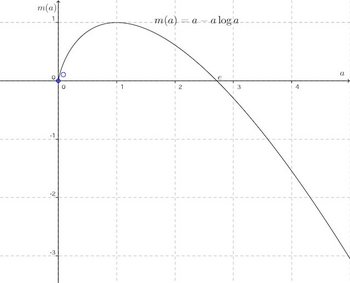
極値の判定は、2階微分をつかって、
(1) f''(loga)=a>0だから極小
(2) m''(1)=−1<0だから極大としてもいいにゃ。
いやまぁ〜、
問題2 方程式の解の個数を求めよ。ただし、aは実数とする。
【解】
x=0は解でないので、
で、を調べるために
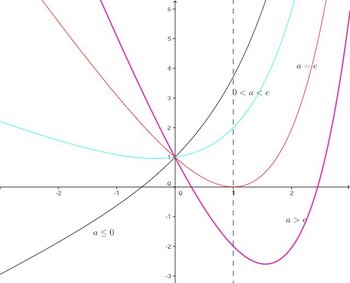
y=f(x)をグラフにすると、次のようになる。
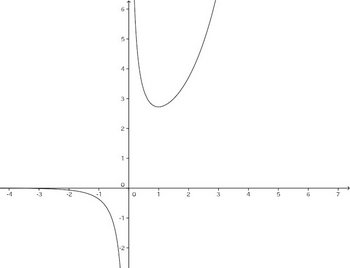
y=aと合せてグラフをかき、y=aとy=f(x)の交点を調べる。
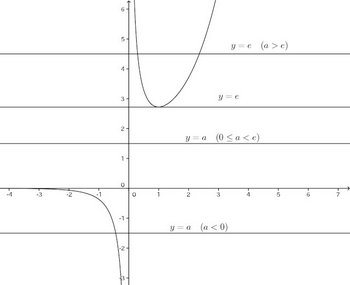
よって、
a<0で解1個
0≦a<eで解なしa=eで解1個
a>eで解2個となる。
【別解】
とy=axの交点を調べるにゃ。
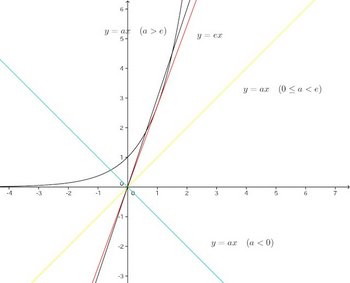
ということで、
a<0で解1個0≦a<eで解なし
a=eで解1個a>eで解2個
となる。【別解2】
問題1の結果を使うにゃ。とし、y=f(x)とx軸との交点を調べるにゃ。
a≦0ならば、f(x)は単調増加。また、f(−∞)=−∞、f(0)=1で、かつ、f(x)は連続なので、中間値の定理より、f(x)=0を満たすxが−∞<x<0の間に一つ存在する。
a>0のとき、x=logaで極小(最小)。で、極小値a(1−loga)だから、0<a<eのとき、極小値>0となり、f(x)>0となって、y=f(x)はx軸と交わらない。つまり、解はない。a=eのとき、x=1で最小となり、最小値は0だにゃ。つまり、x=1が解となり、解は1個。
a>eのとき、x=aで最小で、a(1−loga)<0。そして、f(0)=1でx<logaでは単調減少なので、中間値の定理より、0<x<logaの間に解が一つ、さらに、loga<xで単調増加でf(∞)=∞だから、loga<x<∞の間に一つ存在する。
くどくどと説明するより、次のグラフを見れば、このことがわかると思うにゃ。
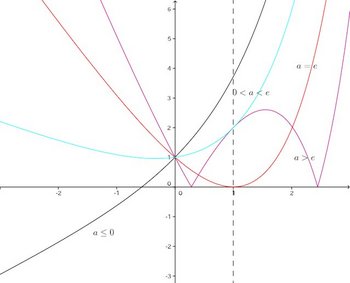
問題3 関数の区間0≦x≦1における最大値が2となるようにaの値を定めよ。ただし、eは自然対数の底である。
【解】
問題1の結果を使うと、a≦eでとなる。
0<a<eのとき、f(x)は0≦x<logaで減少、かつ、loga<x≦1で増加だから、最大値になりうるのはx=0かx=1。f(0)=1なので、f(1)=2とすると、
a=eのとき、0≦x<logaで減少なので、f(0)=1が最大値。
a>eのとき、
ということで、答はa=e−2とa=e+2。
番外編 微分積分の問題を解く4 [ネコ騙し数学]
番外編 微分積分の問題を解く4
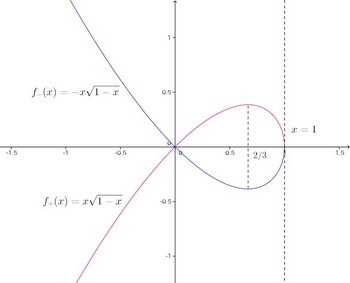
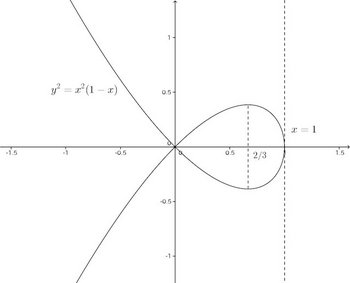
問題 y²=x²(1−x)のグラフをかけ。
【解】
x=2/3のとき、y=f''(2/3)<0なので極大となり、
x=1は漸近線。
dy/dxの計算法は、この他に2つほどある。
もうひとつの方法は、偏微分のところで出てきた陰関数定理を使う方法。
第19回 陰関数と陰関数定理
http://nekodamashi-math.blog.so-net.ne.jp/2015-09-25-1
番外編 微分積分の問題を解く3 [ネコ騙し数学]
番外編 微分積分の問題を解く3
今日も、ネムネコがお絵描きソフトを使いこなせるようになるための練習として、大昔の大学入試で出た問題をもとにグラフなどを作成し、問題を解くことにするにゃ。
問題1 関数
について、
(1) f(x)の極小値が0となるように定数cの値を定めよ。(2) (1)で得られたcの値に対して、曲線y=f(x)、x軸およびy軸で囲まれる部分の面積を求めよ。
【解】
c=0のときのグラフは次の通り。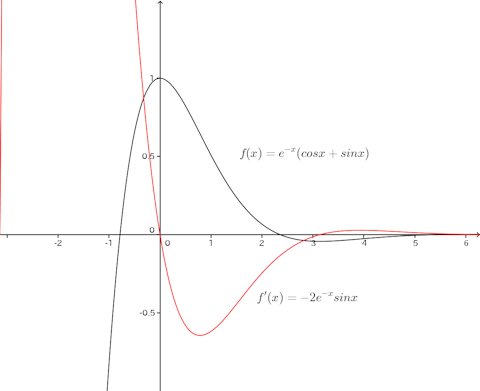
これを見ると、x=πのあたりで極小になることが分かるよね。
(1)
極値になるためにはf'(x)=0でなければならないから、x=0、π、2πが極小値の候補になる。
上のグラフの赤紫の曲線がこのf'(x)。で、極小のとき、f'(x)の符号が−から+に変わるので、この図からx=πが極小であることが分かるにゃ。
ということで、
なお、極値の判定でf(x)の2階微分を使ってもいいにゃ。
ちなみに、
f'(a)=0、f''(a)<0のとき、x=aで極大
f'(a)=0、f''(a)>0のとき、x=aで極小
(2)
http://nemuneko-gensokyou.blog.so-net.ne.jp/2015-03-30-3
に原始関数の表があるにゃ。
最後の2つの式に対してa=−1、b=1とすると、
あるいは、
ということで、
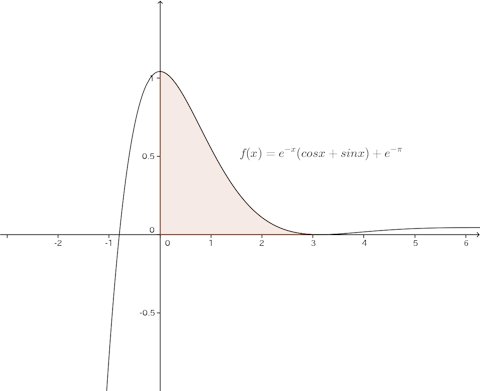
問題2 nを自然数として、
(1) の極値、凹凸を調べてグラフの概形をかけ。
(2) 曲線とx軸で囲まれた部分の面積を
とするとし、
を求めよ。
お絵描きソフトでn=1、2、3、4についてのをかかせると、次のようになる。
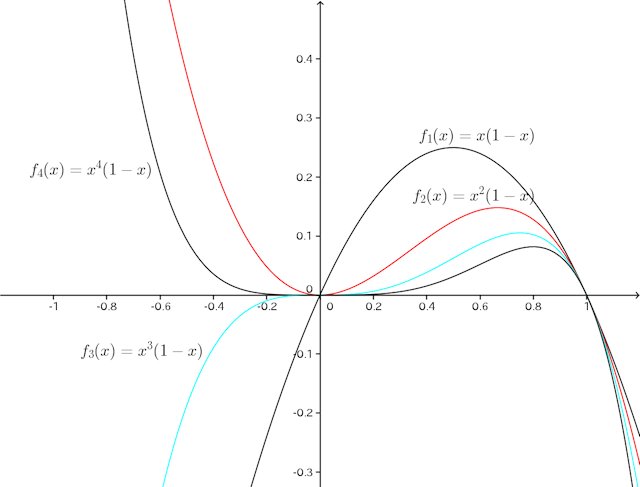
このグラフからnが偶数、奇数のとき、曲線の凹凸がx≦0で違うことが分かるよね。
(1)
で、nが偶数のとき、x=0が極小値になる。
また、nが奇数(n>1)のとき、変曲点はx=0と。
nが偶数のとき、変曲点は。



ちなみに、f''(x)>0のとき凸、f''(x)<0のとき凹
(2)
ねこ騙し数学番外編 微分積分の問題を解く2 [ネコ騙し数学]
ねこ騙し数学番外編 微分積分の問題を解く2
問題1 曲線
【解】
曲線と原点を通る接線との交点をP、そのx座標をx=tとする。
接線の方程式は
だから、
になる。これが原点(0,0)を通るので、
となる。ということで、接線の方程式は
ということで、求める面積Sは
問題2
(1) 曲線の変曲点における接線の方程式を求めよ。
(2) (1)の曲線とその変曲点における接線とy軸とで囲まれた部分の面積を求めよ。
【解】
(1)とする。
(2) 求める面積Sは
ねこ騙し数学番外編だケロ!! 時間つなぎのために微分積分の問題を解いてみた [ネコ騙し数学]
ねこ騙し数学 番外編
ベクトル解析のあと、何をやるか決めていないので、決まるまでの場繋ぎとして、大昔の大学入試に出た微分積分の問題をちょっと解いてみるにゃ。
問題1 f(x)、g(x)は微分可能な関数、またf(x)の導関数f'(x)も微分可能とする。0≦x≦1に対し、
で、f'(1)≧0、f(0)≧0であるならば、f(x)(0≦x≦1)であることを証明せよ。
【解】
よって、
よって、
大学の入学試験でこういう問題が出たら、難しくはないけれど、受験生は意外に青ざめるかもしれない。
さらに、ネムネコが新たに仕入れた数学のお絵描きソフトを習得するための問題を一つ。
問題2 曲線y=logxと、点(0,1)を通るこの曲線の接線と、x軸とで囲まれる図形の面積を求めよ。

【解】
曲線y=f(x)=logxとその接線の接点Pのx座標をx=tとする。そうすると、Pの座標は(t,logt)となる。
よって、接線の方程式は
だから、囲まれる面積は
となる。
なのですが、馬鹿正直に積分の計算をする必要はない。
図を見れば分かる通り、三角形PQRの面積から薄紫の部分を引いたものが求める面積。
三角形PQRの面積は底辺×高さ÷2だから
三角形PQRの面積=(QR)×RP÷2=(2e²)×2/2=2e²と簡単に求まる。
そして、これは
と同じもの。
だから、
と計算してもいい。