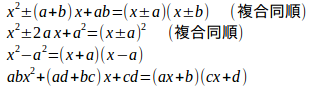第11回 2次方程式と解の公式 [ネコ騙し数学]
第11回 2次方程式と解の公式
二次方程式の話をする前に、次のことを確認しておくにゃ。
§ 二次方程式
2次方程式とは2次の多項式で表される方程式のことで、そのの一般形は次のようになる。
たとえば、
あるいは、4を右辺から左辺に移項し、
例1 次の二次方程式を解け。
x²−3x+2=0を平方完成する。
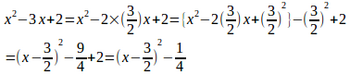
よって、
例1のように因数分解が簡単にできる場合は、例1を見れば分かるように因数分解をして二次方程式を解いたほうが楽。しかし、次の例のように簡単に因数分解ができない場合がある。
例2 次の方程式を解け。
【因数分解による解法】
足して2になる、つまり、a+b=2で、掛けて−1になる、つまりab=−1になるaとbは何だろう(・・?因数分解を利用した解法だと、ここで行き詰まってしまう(^^ゞ
【平方完成による解法】
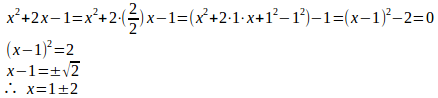
例2を見れば分かるように、【平方完成による解法」の方が利用範囲は広い。だけど、いちいち、平方完成するのは面倒くさい。
ということで、公式を作るにゃ。§ 解の公式
二次方程式の一般形は
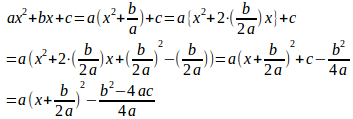
ということで、
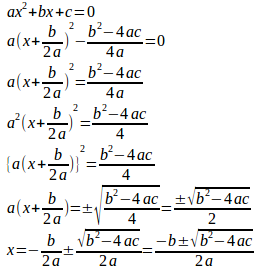
この最後の式が、二次方程式の解の公式と呼ばれるもの。
そして、この解の公式を覚えておけば、いかなる二次方程式の解も求めることができる。
例2の場合、a=1、b=−2、c=1だから
ちなみに、
問題1 次の二次方程式を解け。
(1) x²−4x+3=0(2) x²-4x+1=0
【解】(1) これは簡単に因数分解できるので、因数分解して解く。
(2) これは簡単に因数分解できないので、解の公式(または、その大本の平方完成)を使って解く。
x²-4x+1=0だから、a=1、b=−4、c=1として、解の公式を使う。
問題2 xについての二次方程式
【解】
x=1が①の解なので、x=1を①に代入すると、
a=4のとき、
独り言ですが、二次方程式をx²+px+q=0とし、その解をα、βとすると、
a=−3のとき、p=0、q=−1。で、一方の解をα=1とすると、解と係数の関係より
同様に、a=4のとき・・・。
第10回 平方根 [ネコ騙し数学]
第10回 平方根
§ 平方根
2乗するとaになる数、すなわち、
の解(根)をaの平方根という。
前回、y=x²をやった。このグラフは次のようになる。
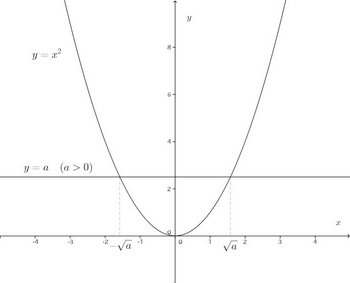
このグラフを見ると、a>0のとき、y=x²=aを満たすxが正と負、2つあることが分かる。
そこで、x²=aを満たす正の数を+√aとし、負の数を−√aと定義する。ただし、x²=0のとき、x=0とする。
つまり、
これは言葉の問題になるのだけれど、「4の平方根」とは「x²=4を満たす実数x」のことで、x=±2となる。aの平方根は、a>0ならば、2つあるにゃ。
対して、√4、すなわち、「ルート4」は2だにゃ。「aの平方根を求めよ」と言われたら、±√aと答えないといけないにゃ。√aだけじゃ〜、駄目だケロよ。
x²=aを満たす方程式の解、根が±√aだから、当然、
また、正数a、bに対して
このことは、2次関数y=x²のグラフより明らかでしょう。
で、さらに、a≧0ならば
§ 有理数と無理数
有理数とは、整数pとqを用いて
そして、有理数は、小数で表した時に、
で、こういうふうに整数の既約分数で表せない数のことを無理数という。この代表的な数として、√2や円周率π、ネイピア数eなどがある。
ということで、√2が有理数でないことの証明をするにゃ。
この証明には、悪名高い「背理法」と呼ばれる証明法が使われるにゃ。【証明】
√2が有理数であると仮定する。
であるとするならば、有理数の定義より
①の両辺を2乗すると、
ところで、先に仮定したように
だけど、分子、分母であるpとqは共通の因数2をもち、既約分数ではない。
――既約分数とは、分子と分母が1以外の公約数を持たない分数。なのに、2という公約数を持っていることになる!!――
何故、このような矛盾が生じたかというと、「√2が有理数である」という仮定が間違っていた、「偽」であったから。よって、√2は無理数である。
(証明終わり)
§ 平方根の計算
a>0、b>0のとき
平方根の分母の有理化
問題1 が6と8の間にあるとき、整数nを求めよ。
【解】
問題2 x=√3−√2、y=√3+√2のとき、x²−xy+y²の値を求めよ。
【解】
真面目に計算してもいいけれど、計算が大変だにゃ。そこで、次のように計算を工夫する。
これは、よく使う計算上のテクニック!!
問題3 √2の小数部分をaとするとき、√32の小数部分をaを用いてあらわせ。
【解】1<√2<2だから、a=√2−1になる(※)。
また、 だから、この小数部分は
(※) √2=1.414・・・=1+0.1414・・・=1+aだから、a=√2−1となる。
第9回 2乗に比例する関数 [ネコ騙し数学]
第9回 2乗に比例する関数
§ 2乗に比例する関数
2乗に比例する関数yがxの2乗、x²に比例する関数のことで、これは次のように表される。
中学校ではこのように教えるらしい。要するに、もっとも簡単な二次関数のことだケロ。
y=x²のとき、値は、次のようになる。
次のグラフを見れば分かる通り、y=ax²のグラフはy軸について対称であり、また、y=ax²とy=−ax²はx軸について対称である。

知っていると思いますが、x²とは
変化率
x=x₁とx=x₂のy=ax²の変化率は
これはもっと簡単になって、
ここからは逸脱になるけれど、もし、x₂が限りなくx₁に近づけば、
あまりに書くことがなかったので、もののついでに書いただけだにゃ。
§ 放物線と直線の交点
y=ax²とy=bx+cの位置関係をあらわすグラフを以下にしめすにゃ。
a、b、cの値によって、2点で交わるときもあれば、1点で接するとき、そして、交わったり接したりしない3つの場合がある。
交点のx座標は、
もっとも、解(実数解)があればだよ、あれば。
中学校では虚数や複素数を数として認めていないからね。この点は重要だケロ。
この流れで一気に解の公式や二次方程式の判別式の話をしてもいいけれど、今はしないにゃ。
問題2 yがxの2乗に比例し、x=2のときy=−12である。このとき、x=−1のときのyの値を求めよ。
【解】y=ax²とする。x=2のとき、y=−12なので、これをy=ax²に代入すると、
問題3 y=ax²のグラフが(4,4)を通るとき、次の問いに答えよ。
(1) aの値を求めよ。
(2) xの値が4から6まで増すときの変化の割合を求めよ。【解】
(1) y=ax²が(x,y)=(4,4)を通過するので、
(2) 変化の割合は
変化の割合は、⑨を使って、次のように計算してもいいケロよ。
問題4
(1) 点Aは原点以外のx座標とy座標が等しい放物線上の点である。点Aの座標を求めよ。(2) 直線ABのy切片が4のとき、この直線の傾きを求めよ。また、点Bの座標を求めよ。
(3) △OABの面積を求めよ。【解】
(1) 点Aのx座標をaとすると、点Aは放物線上にあるので、点Aのy座標はy=a²/2となる。
(2) 直線ABの傾きは
(3) △OABの面積は△OCAと△OBCの面積の和。
(2)でBのy座標と求めるとき、直線の方程式を使って
第8回 直線 [ネコ騙し数学]
第8回 直線
これまでやってきたことの復習と”まとめ”をかねて、中学数学の延長として高校数学の内容を少し含めて話をするにゃ。
1 直線の方程式
(1) 傾きa、y切片bの直線 y=ax+b(2) 点(x₀,y₀)を通り、傾きaの直線 y−y₀=a(x−x₀)
(3) 2点(x₁,y₁)、(x₂,y₂)を通る直線の方程式
(4)の式ははじめて出てきたと思うんで、これだけ、説明することにする。
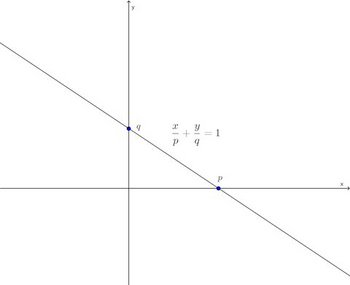
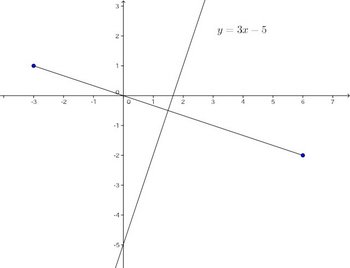
x切片とは、直線とx軸(y=0)の交点のx座標のこと。だから、(4)の直線は2点(0,q)、(p,0)を通る直線。(x,y)=(0,q)、(x,y)=(p,0)を
論より証拠というわけで、次の図を見れば、このことが分かるにゃ。
2 2直線の位置関係
2直線y=mx+n、y=m'x+n'について(1) 平行条件 m=m' (さらに、n=n'ならば2直線は一致)
(2) 垂直条件 mm'=−1ネムネコは、高校数学の教科書を持っていないので、教科書で(2)の垂直条件をどのように導いているかは知らない。だけれども、ベクトルを使うのならば、y=mx+nの方向ベクトル、y=m'x+n'の方向ベクトル
になる。この2直線が垂直なので、この2つの方向ベクトルが垂直ということになり、ベクトルの内積を使うと、
中学レベルの知識を使ってこのことを示そうと思ったけれど、これは図に頼った証明になるのでやめるにゃ。mとm'が異符号であることを無前提に使っているから、こういう証明はちょっと危ないにゃ(^^)
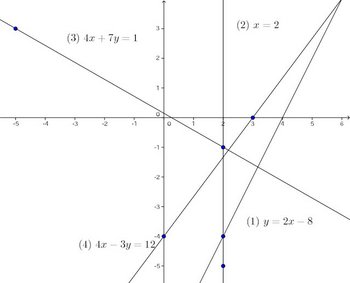
問題1 次の直線の方程式を求めよ。
(1) 傾きが3で点(2,−4)を通る。(2) 点(2,−5)を通りy軸に平行な直線。
(3) 2点(−5,3)、(2,−1)を結ぶ直線。(4) x切片が3、y切片が-4。
【答】
問題2 2直線y=2x+a+3、y=3x+2aが第2象限で交わるためのaの値の範囲を求めよ。
【解】2直線y=2x+a+3、y=3x+2aの交点を求める。
問題3 次の直線の方程式を求めよ。
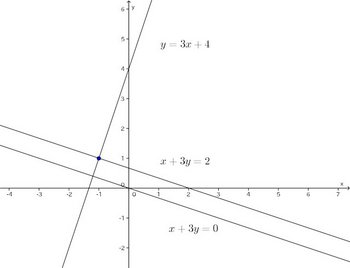
(1) 点(−1,1)を通り、直線x+3y=0に平行な直線および垂直な直線。(2) 2点(6,−2)、(−3,1)を結ぶ線分の垂直2等分線。
【解】(1)
に垂直な直線の傾きをmとすると、
(2) 欲しいのは2点(6,−2)、(−3,1)を結ぶ直線の方程式ではなく、傾きだけだケロ。ということで、傾き求める。
ということで、中点求める。
第7回 二元一次方程式のグラフと連立一次方程式 [ネコ騙し数学]
第7回 二元一次方程式のグラフと連立一次方程式
§ 二元一次方程式のグラフ
二元一次方程式の一般形は、
a≠0、b≠0のとき、①は
となり、傾きがでy切片が
の直線になる。
b=0のとき
いずれにせよ、ax+by=cを満たす(x,y)は直線の方程式になる。
例
(1) 5x−3y=−15これをyについて解くと、
(2) y=5
(3) x=2
グラフで表現すると、次のようになる。

問題 直線kx−y=3kについて
(1) y切片が3であるときのkの値を求めよ。(2) 直線y=2x+1と平行となるようなkの値を求めよ。
(3) kがいろいろな値をとるとき、この直線はある決まった点(不動点)を通る。その点の座標を求めよ。【解】
(1) kx−y=3kにx=0、y=3を代入すると、
(2)
(3)
§ 二元一次方程式のグラフと連立方程式の解
次の二元一次連立方程式があるとする。
具体的な例をだしたほうがわかりやすいので次の連立方程式を考えることにする。
②が①の0以外の定数倍のときも事情は同じ。
つぎに、
①は傾き−2でy切片は3。②は傾き−2でy切片は5。傾きが同じなので、①と②の直線は平行で、この②直線が交わることはない。つまり解はない(不能)。
といことで、
このことは行列を使うとわかりやすい、この連立方程式を行列で書くと
で、もし
Aが逆行列をもつ条件は、
今、書いている部分の話は、中学の数学の範囲を超えているので、①と②が平行のとき、この連立方程式は解けない、ということだけを覚えて欲しい。
――内緒話だが、③はが平行でない必要十分条件!!――
問題2 2直線x+y=6、x+ay=−6が直線y=2x上で交わるとき、aの値を求めよ。
【解】x+y=6とy=2xは、互いに平行じゃないから解を持つケロ。
だから、まずこの交点を求めるにゃ。
この(2,4)をx+ay=−6が通過するので、
問題3 −x+y=1、x+y=3、y=k(x+3)が三角形を作らないようにkの値を定めよ。
【解】−x+y=1、x+y=3の交点は(1,2)。この点をy=k(x+3)が通過するとき三角形にならないケロ。
だから、
−x+y=1とy=k(x+3)が平行のとき、この2直線は交わらない。ということで、k=−1。
同様に、x+y=3とy=k(x+3)が平行のときにもこの2直線は交わらない。よって、k=1。だから、答えは

2016-04-16 11:5
第6回 一次関数とそのグラフ [ネコ騙し数学]
第6回 一次関数とそのグラフ
§一次関数
一次関数とは、2つの変数xとyの関係が
上の式から明らかなように、b=0のときは、y=axとなり、yはxに比例する。
(x₁,y₁)、(x₂,y₂)という点がy=ax+bを満たすならば、
このことは、y=ax+bをグラフに描いた次のものを見ればよくわかると思う。
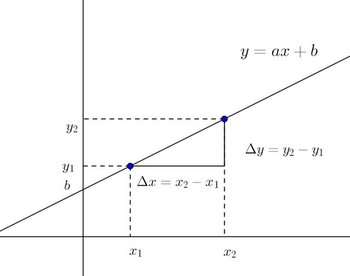
また、②にこの結果を代入すれば、
そして、これは、2点、(x₁,y₁)、(x₂,y₂)を通る直線の方程式と呼ばれるものだケロ。
④式は高校の数学の範囲になるので、中学数学に戻ることにするにゃ。
問題1 yはxの一次関数で、xの値が1増すごとにyの値は3ずつ増し、x=2のときy=−1である。この一次関数を求めよ。
【解】
この一次関数をy=ax+bとする。
このとき、
§一次関数のグラフ
一次関数y=ax+bのグラフは、直線y=axに平行で、点(0,b)を通る直線。このaを直線の傾き、bをy切片という。
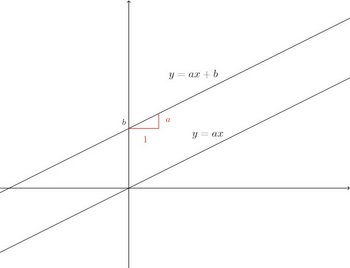
これも中学の範囲を逸脱するけれど、傾きがmで点(x₀,y₀)を通る直線の方程式は
上の式にx=x₀を代入すれば、y=y₀になるし、y=y₀を代入すれば、x=x₀になることから、これが条件を満たしていることは明らかでしょう。
ちなみに、2直線
では、問題。
問題2 次の直線を求めよ。
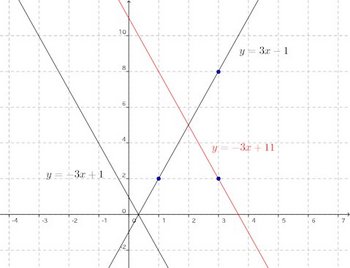
(1) y=−3x+1に平行で、点(3,2)を通る直線。(2) 2点(1,2)、(3,8)を通る直線。
【解】(1) y=−3x+1と平行な直線なので、傾きは−3。
で、⑤を使うのならば、(x₀,y₀)=(3,2)なので
(2) この直線の方程式をy=ax+bとする。
この直線は2点(1,2)、(3,8)を通るので、x=1、y=2、さらに、x=3、y=8を代入すると、
代入法を使って上の連立方程式を解いてもいいけれど、②から①を引くとbが消えるので
①と②のどちらにa=3を代入してもいいけれど、①の方が計算が楽なので①に代入し、
④を使うならば、(x₁,y₁)=(1,2)、(x₂,y₂)=(3,8)として、
あるいは、傾きaは
x=3、y=8のときは
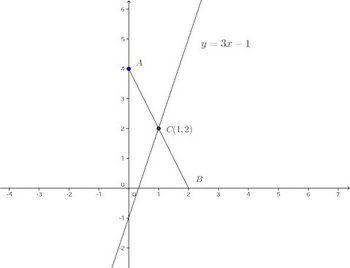
問題3
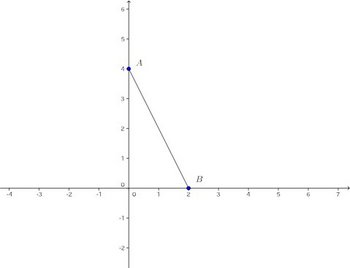
(2) 直線y=3x+bが線分ABの中点を通るようにbの値を定めよ。
【解】
(1) 図よりy切片は4。傾きは
(2) 中点の座標は
第5回 比例・反比例 [ネコ騙し数学]
第5回 比例・反比例
§比例
比例2つの変数、xとyの間に次のような関係があるとする。
このとき、yはxに(正)比例するといい、定数aを比例定数という。
これはy=3xという関係があり、yはxに比例し、比例定数a=−3となる。
aは、定数だから、当然、変化しない。もし、xとyの値によってaの値が変わるのならば、xとyは比例関係にないことになる。
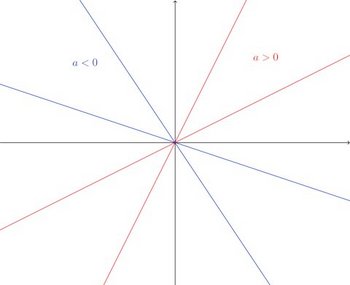
y=axのグラフから明らかなように、a>0ならば右上がりの原点を通る直線となりa<0ならば右下がりの原点を通る直線となる。
問題1 yはxに比例し、x=3のときy=−6である。x=−4のとき、yの値はいくらか。
【解】y=axとすると、x=3、y=−6なので、
よって、x=−4のとき
たぶん、こう解くのが模範解答なのでしょう(^^ゞ
【別解1】
x=−4のときのyの値をyとする。xとyは比例関係にあるので、
【別解2】
小学校レベルの知識を使うならば、
どう解かなければならないということはないだろう。一番楽なのは別解1だと思うけれど、別解2で解いても構いやしない(笑)。
問題2 直線y=axが点A(1,2)と点B(3,1)を結ぶ線分ABを通るとき、aはどんな範囲の数か。
【解】こういう時こそ、グラフの出番だケロ。
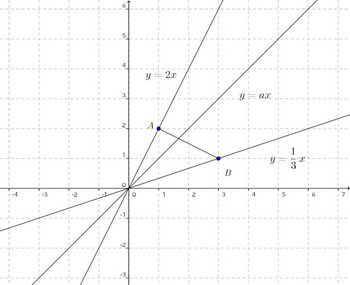
この図からほとんど明らかだけれど、aが最小の時は点B(3,1)を通るときで、aが最大の時はA(1,2)を通るとき。
点Bを通るとき、
§反比例
反比例
2つの変数、xとyに次の関係があるとき、yはxに反比例するという。
グラフは次のようになる。
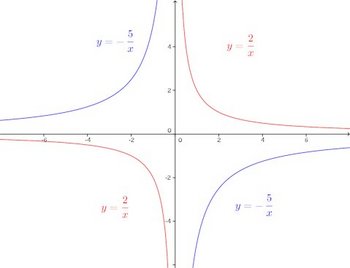
a>0のとき、y=a/xの曲線は第1象限、第3象限にあり、a<0のときy=a/xは第2象限、第4象限にある。また、この曲線は原点について対称である。
問題3 反比例をあらわすグラフが点(1.5,8)を通るとき、このグラフ上の点(x,y)で、x、yがともに整数である者はいくつかるか。
【解】反比例なのだから
こんな問題ばかり解いていると⑨になりそうだにゃ(>_<)。
問題 x>0で定義された
このとき、
(1) Pは線分ABの中点であることを示せ。(2) △OABの面積は点Pの位置によらず一定であることを示せ。
【解】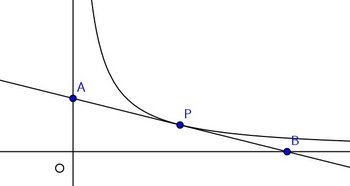
接線の方程式は、
(1) 線分ABの中点を求めると
(2) △OABの面積Sは
この問題は、ひょっとしたら微分積分の時にやったかもしれないけれど、面白い性質なんじゃ〜あるまいか。
そして、こうしたことを面白い、何故だろうなんだろうと思う感性は大切なんじゃなかろうか。
第4回 関数と座標 [ネコ騙し数学]
第4回 関数と座標
§関数
ともなって2つの変わる量個数(個) | 1 | 2 | 3 | 4 | 5 | 6 |
代金(円) | 80 | 160 | 240 | 320 | 400 | 480 |
上の例の個数と代金のように、一つの量が変わるに連れてもう一方の量が変わるような量をともなって変わる2つの変わる量という。
いろいろと変わる数量を一つの文字であらわし、いろいろな値をとる文字を変数、変数の取りうる範囲を変域という。
上の例で、個数をx、代金をyとすると、xとyの間にはy=80xという関係がある。xの変域 {1, 2, 3, 4, 5, 6}
yの変域 {80, 160, 240, 320, 400, 480}関数
変数x、yがあって、xの値を決めるとyの値がひとつだけに決まるとき、yはxの関数という。中学では、このように関数を教えるらしい。難しいケロ。
問題1 まわり40cmの長方形がある。縦の長さをxcm、横の長さをycmとして、次の問いに答えよ。
(1) yをxの式であらわせ。(2) x=5のときのyの値を答えよ。
(3) yはxの関数と言えるか。【解】
(1) 2(x+y)=40だからx+y=20。よって、y=20−x。(2) x=5のとき、y=20−x=20−5=15。
(3) xの値が与えられるとyの値もただひとつ決まるので関数である。
この問題にはないけれど、xの変域(定義域)は0<x<20、yの変域(地域)も0<y<20。
§座標
座標下の図で、横の数直線をx軸、縦の数直線をy軸といい、x軸とy軸を合せて座標軸という。さらに、x軸とy軸の交点を原点と言いOであらわす。
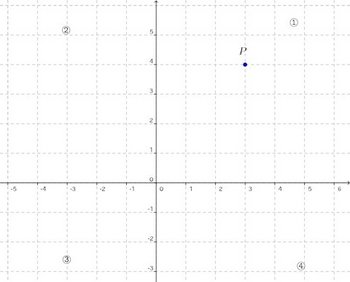
点の座標
上の図の点Pの位置は、Pからx軸、y軸におろした垂線と座標軸の交点の座標(?)3と4をの組(3,4)をPの座標という。また、3をPのx座標、4をPのy座標という。象限
座標軸で分けられた4つの部分。上図の①を第1象限、②を第2象限、③を第3象限、④を第4象限という。
§中点
2点(x₁,y₁)、(x₂,y₂)の中点の座標は
(a,b)とx軸について対称な点は(a,−b)、y軸について対称な点は(−a,b)であり、原点について対称な点は(−a,−b)である。
問題2 点(3,−2)について、点(1,2)と対称な点の座標を求めよ。
【解】対称な点の座標を(x,y)とする。このとき、
問題3 点A(2,4)、B(6,2)がある。
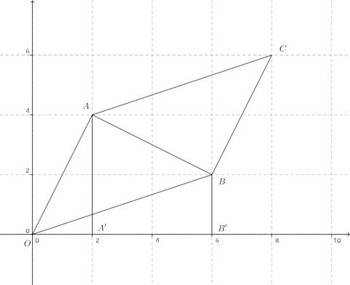
(1) 点Aと原点Oについて対称な点の座標を求めよ。(2) 平行四辺形AOBCをかき、点Cの座標を求めよ。
(3) 平行四辺形AOBCの面積を求めよ。(1) (−2,−4)
(2) (8,6)
(3) A、Bからx軸への垂線をおろし、x軸との交点をA'、B'とする。△AOB=△AOA'+台形AA'B'B−△BOB'
になる。
中学の範囲を超えるけれど、ベクトルを使うならば、
で、
だから、
中学数学 第3回 不等式 [ネコ騙し数学]
第3回 不等式
不等式の性質
(1) aとbの大小関係は、a>b、a=b、a<bのうちのどれか一つが成立する。(2) a>b、b>cならばa>cである。
(3) a>bならばa+c>b+cである(cは任意の実数)。(4) a>bのとき、c>0ならばac>bc、c<0ならばac<bc
これは数(実数)の公理みたいなものだから、何故、これは無条件で受け入れてもらわないと困るにゃ。
例題 a>b、c>dのとき、a+c>b+dであることを証明せよ。
【証明】a>bならばa+c>b+c
c>dならばb+c>b+dよって、
a+c>b+c、b+c>b+dならば、a+c>b+d(証明終わり)
では、不等式の基本的性質に関する問題。
問題1 次のことは一般に成り立たない。成り立たない例(反例)をあげよ。
(1) a>c、b>cならばab>c²
(3) b/a>1ならばb>aである。
【解】大体、こういう時は、マイナスの数の掛け算(割り算)が関係しているにゃ(^^)
ということで、(1) a=b=1、c=−2。
(3) b=−2、a=−1(2) a=1、b=0
問題2 a+b>c、b+c>a、c+a<bのとき、a、b、cの間にはどの関係が成り立つか。
(1) a>b>c (2) b>c、a>c (3) b>c、b>a(4) b>c>a (5) b>a>c
【解】成り立つのは(3)だけ。
a+b>c、b>c+aより、
(3)以外が成り立たない反例として、a=c=0、b=1を上げればいいにゃ。
問題にはないのだけれど、
a+b>cとb+c>aより
問題3 次の問を答えよ。
(1) 不等式2x−8>4x+5の解のうちで、最も大きい整数を求めよ。
(2) ある数xの5倍から6を引いた数は、xの3倍に2加えた数より小さい。xはどんな範囲の数か。【解】
(1)
(2) 5x−6<3x+2
これを解くと、
問題4
【解】
これを満たす整数xは7、8。
x=7のとき
中学数学 第2回 連立一次方程式 [ネコ騙し数学]
中学数学 第2回 連立一次方程式
連立方程式とは、方程式が2つ以上組み合わされたもの。次のように
連立2元一次方程式の一般形は、
で、連立一次方程式の解法としては、代入法、加減法と呼ばれるものがある。
代入法の例
①をyについて解くと
加減法の例
①と②をじっと見て、最初にどちらを消去したいか考える。この場合、どっちでも似たようなものなので、yを消去することにする。
yの係数の絶対値を同じにするために、①に3を掛け、②に2をかける。

「何で、オレがこんな計算をしなければならないんだ」と、だんだん腹が立ってくる(^^ゞ
問題1 aをbで割ると商が3で余りが8になり、aの3倍をbで割ると商が11で余りが2になるような、2つの正数があるか。あればその2数を求めよ。
【解】(割られる数)=(割る数)×(商)+(余り)
だから、
a=41、b=11は題意を満たすので、a=41、b=11である。
問題2 y=ax+bと表される等式で、x=2のときy=1、x=5のときy=10である。a、bの値を求めよ。
【解】x=2のとき2a+b=1、x=5のとき5a+b=10。
②から①を引くとbが消えるケロ。
――ケロケロしないと、ネムネコの精神の均衡が保てない!!――
この問題2は2点を通る直線の方程式を求めている。
このことは、次の図を見るとよくわかると思う。
直線の傾きaは