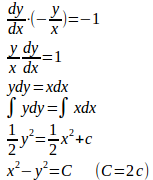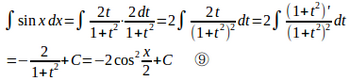微分方程式の応用1 [ネコ騙し数学]
微分方程式の応用1
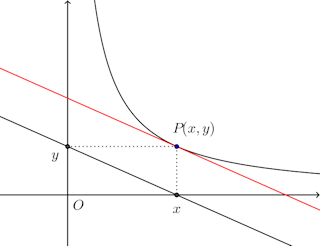
問題1 曲線上の1点Pにおけるその接線がx軸と交わる点をTとするとき、線分PTがいつもy軸によって2等分されるという。この曲線を求めよ。
【解】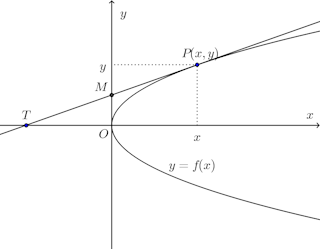 曲線上の点Pの座標を(x,y)、Pにおける接線上の点を(X,Y)とすると、接線の方程式は
曲線上の点Pの座標を(x,y)、Pにおける接線上の点を(X,Y)とすると、接線の方程式は
すなわち、
(解答終了)
問題2 曲線上の1点Pからx軸、y軸におろした垂線の足をQ、Rとするとき、次の問いに答えよ。
(1) Pにおける接線がいつも直線QRと平行になっている曲線を求めよ。
(2) Pにおける接線がいつも直線QRと垂直になっている曲線を求めよ。
(3) Pにおける接線と直線QRとの交点をSとするとき、Sがy軸に平行な一定直線x=aの上にある曲線を求めよ。
【解】(1) Qの座標は(x,0)、Rの座標は(0,y)だから直線QRの傾きは
すなわち、
(2) 点Pにおける曲線の接線と直線QRが垂直だから、接線の傾きと直線QRの傾きの積は−1である。
すなわち、(3) 点Pにおける曲線の接線の方程式は、とすると、
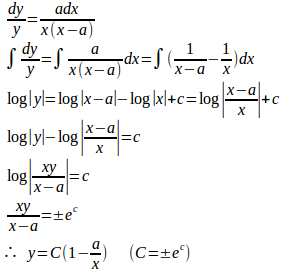
(解答終了)
問題3 次の曲線群のすべてと直角に交わるような曲線の方程式を求めよ。
(1) y²=4px (pは任意定数でp≠0)(2) xy=a (aは任意定数でa≠0)
【解】(1)
y²=4pxをxで微分すると
よって、求める曲線は、
(2) xy=aをxで微分すると
難しい微分方程式の解法 [ネコ騙し数学]
難しい微分方程式の解法
次の微分方程式があるとする。
①の両辺に
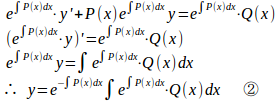
と、①の一般解を求めることができる。
このことを念頭に置き、次の問題を解くことにする。問題1
(1) 微分可能な任意の関数f(x)に対して
(2) 次の微分方程式の解で、f(0)=1になるものを求めよ。
(1)
よって、
(2) (1)で求めたを微分方程式にかけると
念のために、が微分方程式の解であるか確かめてみると、
また、問題1の(2)は、先に紹介した微分方程式
ちなみに、
問題2
微分方程式
【解】
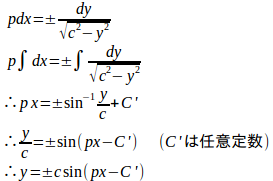
ここで、
微分方程式の解法3 [ネコ騙し数学]
微分方程式の解法3
§1 定数係数の2階線形微分方程式の解法
高校の微分積分では、定数係数の2階微分方程式
ではあるが、結論を先取りして言うならば、①の解は、2次方程式――特性方程式という――
このことは知っておいて損はないだろう。
③が①の解になることは、
同様に、も解であり、
また、逆に①がという形の解をもつとすれば、
粗い議論であるが、2次方程式①が相異なる②実根α、βをもつとき、微分方程式①の解が③になることを理解できるのではないか。
1階の微分方程式
そして、この場合も一次方程式
しかし、この結果は高校の数学の範囲を超えているので、高校の微分積分ではこの解法を採用しないことにする。ではあるが、この議論は、微分方程式の解の確認に使えるので、知ったおいて損はないと思う。
問 次の微分方程式の解を求めよ。
【解】
(1) 特性方程式を解くと
(2) 特性方程式
§2 連立微分方程式の解法
問題1 f'(x)=g(x)、g'(x)=f(x)、f(0)=1、g(0)=0を満たすような関数f(x)、g(x)を求めよ。
f(x)=y、g(x)=zとおくと、
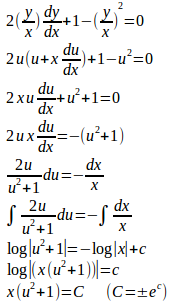
したがって、
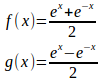
(解答終了)
このように解くことができるけれど、これは高校数学の範囲がの解法なので、この問題は次のように解くとよい。
【解】
u=f(x)+g(x)とおくと
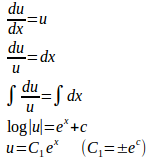
①−②
v=f(x)−g(x)とおくと
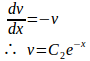
⑤−⑥
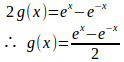
(解答終了)
問題2 平面上を運動するP(x,y)の両軸方向の速度について
の関係があるとき、Pはどのような曲線上を動くか。
【解】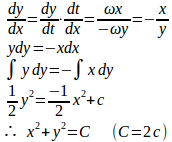
(解答終了)
この連立微分方程式の解を求められないことはないのだけれど、これは高校の微分積分の範囲を大きく逸脱してしまうので、これ以上は解かないことにする。
微分方程式の解法2 [ネコ騙し数学]
微分方程式の解法2
§1 同次形微分方程式の解法
高校の微分積分の範囲外なのだけれど、同次形の微分方程式の解法を紹介することにする。
1階の同次形の微分方程式の基本形は
y=uxとおくと、
問題1 次の微分方程式を解け。
y=uxとおくと
(1) 両辺をxで割ると
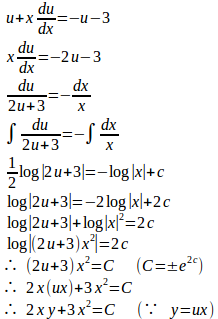
よって、解は
(2)
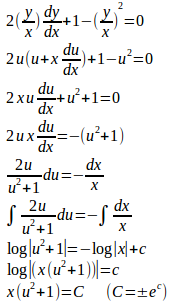
u=y/xだから、
§2 積分を含む関数方程式の解法
F'(x)=f(x)とすると、定積分は
したがって
問題2 次の条件を満たす微分可能なf(x)を求めよ。
(1) 両辺をxで微分すると
(2) 両辺をxで微分すると
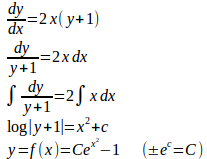
また、
問題2の場合、微分方程式に初期条件を与えられることに注意。
微分方程式の解法1 [ネコ騙し数学]
微分方程式の解法1
高校の微分積分で扱う微分方程式の解法は次の2タイプ。
タイプ1 直接積分形
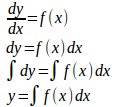
タイプ2 変数分離形
この2つのタイプのいずれか。
タイプ1は次のように変数分離法を用いて微分方程式の解を求めることができる。
問題1 次の微分方程式を解け。
(1)
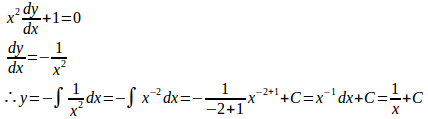
(2)
――(註) 積分定数は省略してある――
したがって、②は
直接積分するのではなく、たとえば、(1)の場合、
問題2 変数分離法を用いて、次の微分方程式を解け。
(1)

(2)
(3)
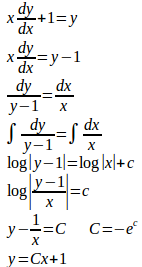
(解答終了)
問題3 次の微分方程式で()内の初期条件を満たす解を求めよ。
(1)
よって、
(2)
よって、
微分方程式2 [ネコ騙し数学]
微分方程式2
問題1 周期が一定の単振動の方程式
【解】
(解答終わり)
問題2 ある物体が大気中で冷却する速さは、その物体の温度と気温の差に比例するという(ニュートンの冷却法則)。
比例定数をk(k>0)として、物体が冷却する微分方程式を作れ。ただし、気温はa℃とする。【解】
時刻tにおける物体の温度をx、時刻t+Δtにおける温度をx+Δxとする。この間に冷えた温度は
この微分方程式の解は、変数分離法を用いて次のように解くことができる。
①が一般解、t=0のときx₀が初期条件、そして②が特殊解(特別解)である。
この微分方程式は物体の冷却という現象だけではなく、たとえば、放射性物質の崩壊、コンデンサーの放電など、自然界では広く成立する微分方程式である。
問題3 曲線y=f(x)は第1象限にあって、この曲線上の任意の点Pにおける接線は、つねにx軸、y軸の両方と交わり、その交点をそれぞれQ、Rとすれば、接点Pは線分QRを2:1に内分するという。
(1) この曲線の満たす微分方程式を求めよ。(2) このような曲線のうち、点(1,1)を通るものを求めよ。
【解】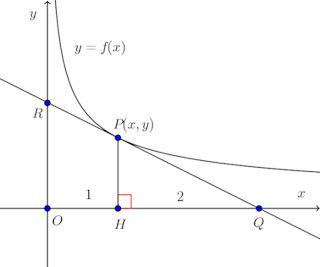 (1) 点P(x,y)における接線の方程式は、(X,Y)を接線上の点の座標とすると、
(1) 点P(x,y)における接線の方程式は、(X,Y)を接線上の点の座標とすると、
(2) ②より
よって、
微分方程式 [ネコ騙し数学]
微分方程式
§1 微分方程式の定義
変数x、その関数y、yの導関数を含む方程式を微分方程式という。
与えられた微分方程式を満たす関数を微分方程式の解といい、解を求めることを微分方程式を解くという。微分方程式がn次の導関数を含み、それよりも次数の高い導関数を含まないときn階の微分方程式という。
一般にn階の微分方程式はn個の任意定数を含む解をもち、階数と同数の任意定数を含む解を一般解といい、一般解の任意定数に特別の値を与えたものを特殊解(特別解)という。特殊解でない解を特異解という。例 y'=yは一階の微分方程式、y''+y=0は2階の微分方程式。はy''+y=0の一般解であり、
は特殊解である。
は
の一般解であり、
は特異解である。
§2 微分方程式の作り方
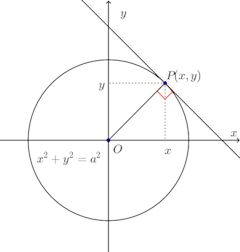
問題1 (1)、(2)の曲線の方程式から任意定数aを消去して微分方程式を作り、微分方程式は方程式のあらわす曲線のどのような性質をあらわしているか答えよ。
したがって、原点Oと円周上の1点Pを結ぶ直線OPとPにおける円の接線は垂直である。
(2) y²=4axをxで微分すると
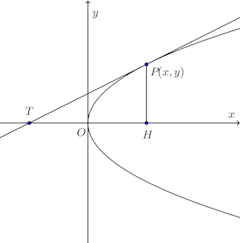 両辺にxをかけると
両辺にxをかけると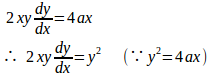
放物線y²=4ax上の点Pの座標を(x,y)とする。
Pからx軸に下ろした垂線の足をH、放物線のPにおける接線とx軸との交点をTとする。接線の傾き=PH/TH
また、OH=xだから、TH=2OHとなり、原点OはTHの中点である。
よって、放物線y²=4axの頂点はTHの中点である。(解答終わり)
少し危険だけれど、(2)の別解(?)として次のものをあげておく。
【別解1】
【別解2】
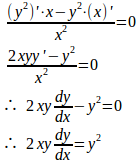
(別解2終わり)
ちなみに、
問題2 x軸に中心を有する半径1の円群に共通な性質をあらわす微分方程式を作れ。
【解】円の中心を(a,0)とすると、半径1の円の方程式は
y=±1は、問題2の微分方程式を満足するので、この微分方程式の解である。しかし、②の一般解である①の形であらわすことができない。このような解を特異解という。
問題3 方程式
【解】
だから、y''≠0。
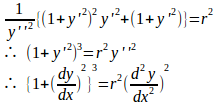
(解答おわり)
問題2の結果をrについて解くと
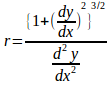
この右辺は曲率半径だから、円は曲率半径、曲率が一定の曲線である。
部分積分 [ネコ騙し数学]
部分積分
f(x)、g(x)を微分可能な関数とすると、
これを部分積分の公式という。
例1
①において、特にg(x)=xのとき
例2
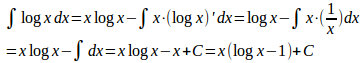
問題1 次の不定積分を求めよ。
(1) f(x)=x、g'(x)=cosxと考えると、f'(x)=1、g(x)=sinx。
よって、
(2) と考えると、
(3) f(x)=logx、g'(x)=xと考えると、
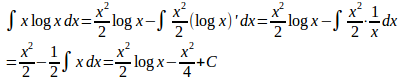
(4) f(x)=logx、g'(x)=1/xと考えると、f'(x)=1/x、g(x)=logx。
よって、 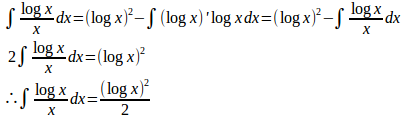
これに積分定数を付けて
(5) f(x)=(logx)²、g'(x)=1と考えると、
よって、 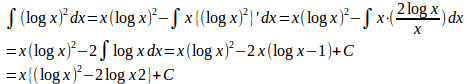
(解答終わり)
(4)については、置換積分を用いて、次のように解くこともできる。
【別解】
t=logxとおくと
問題2 次の不定積分を求めよ。
とすると、
については、
と考えて
①と②より
置換積分4 三角関数を含む置換積分 [ネコ騙し数学]
置換積分4 三角関数を含む置換積分
§1 三角関数を含む置換積分の基本
のタイプは、sinx=tとおくと、cosxdx=dtだから
のタイプは、cosx=tとおくと、−sinxdx=dtだから
問題1 次の不定積分を求めよ。
(1)
したがって、cosx=tとおくと、−sinxdx=dt
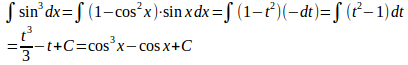
(2)
したがって、cosx=t、−sinxdx=dt
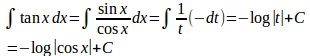
(3)
したがって、cosx=tとおくと、−sinxdx=dt
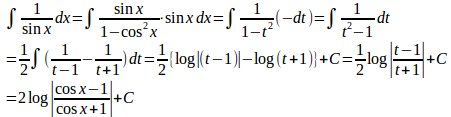
(解答終わり)
(2)については、3倍角の公式
§2 一般的な方法
ではなく、より一般的な
のタイプの積分は、
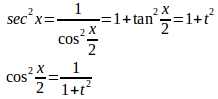
から
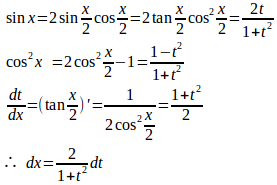
したがって、
以上のことをまとめると、
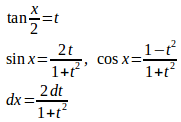
として、これを代入すると
この方法を用いれば、§1で示した三角関数の積分はもちろん、より一般的で複雑な積分も行なうことができる。
例 次の不定積分を求めよ。
とおくと
(解答終わり)
この結果は、
いえいえ、この2つは同じものです。
⑨を次のように変形すれば、同じものであることが分かる。
問題2 上記の方法を用いて、次の不定積分を求めよ。
tan(x/2)=tとおくと
問題1の(3)と見た目は違いますが、この両者は同じものです。
同じものであることを確かめるように。§2の方法は、どうしても不定積分が求まらないときの最終手段ともいうべき方法なので、安易に使わないほうがいい。
一般的に、この方法を用いると計算が複雑になるだけではなく、見た目の違う結果が得られて、同じものかどうか判断しにく、混乱してしまう。置換積分3 [ネコ騙し数学]
置換積分3
置換積分には、このタイプの積分には、このように変数を変換せよ、というものがあるので、その代表的なものを紹介することにする。
タイプ1 を含む積分
とおき、
問題1 次の不定積分を求めよ。
とおくと
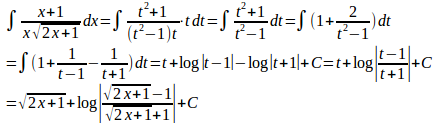
(解答終了)
タイプ2 を含む積分
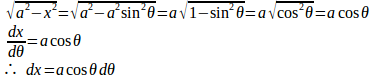
になる。
問題2 次の不定積分を求めよ。
x=asinθとおくと
おまけとして
問題3 次の不定積分を求めよ。
x=atanθとおくと
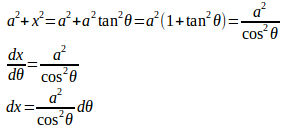
したがって、
タイプ3 を含む積分
とおくと
問題4 次の不定積分を求めよ。
タイプ3の不定積分は、高校数学の範囲を逸脱しているので、おぼえる必要はないが、この方法を知らないと、このタイプの不定積分を求めることは極めて難しい。
こういうアクロバティックな変数の変換法があることを十分だと思う。ただ、タイプ2の置換積分は、定積分で何度も登場するので、これだけはおぼえて欲しい。