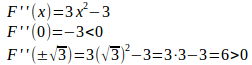ワンポイントゼミ１９

ワンポイントゼミ１９

問題　x軸上を動く点Pとy軸上を動く点Qがある。点Pは原点を出発しt秒後の速度がsin2tであり、点Qは点(0,1)を出発しt秒後の速度がsintである。このとき線分PQの中点Rの軌跡を図示せよ。ただし速度は座標軸の正の方向とする。

【考え方】

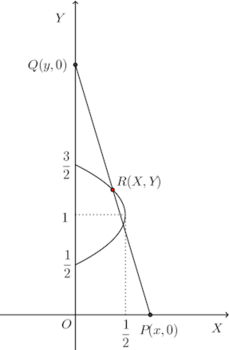点P、Qの座標をそれぞれ(x,0)、(0,y)とする。

点Pのt秒後の速度はsin2tだから

　　

点Qのt秒後の速度はsintだから

　　

つまり、

　　

①、②をtで積分すると

　　

t=0のとき、x=0、y=1だから、

　　

したがって、

　　

RはP、Qの中点だから

　　

三角関数の倍角公式より

　　

だから、③は

　　

④より

　　

これを⑤に代入すると

　　

ところで、

　　

よって、③式から、Xは、cos2t=−1のとき最大、cos2t=1のとき最小で、

　　

となる。

よって、求める軌跡は

　　

である。

ちなみに、

　　

ax=sとおくと、

　　

したがって、

　　

同様に、

　　

置換積分２

置換積分２

今回は、置換積分を用いて、不定積分を求めることにする。

置換積分の基本公式は次のとおりである。

x=g(t)とおくと

　　

問題１　次の不定積分を求めよ。

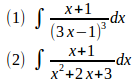
【解】

（１）　t=3x−1とおくと、

　　

よって、

　　

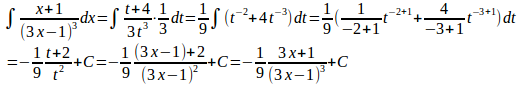
（２）　t=x²+2x+3とおくと

　　

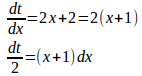
よって、

　　

（解答終了）

（２）については、f(x)=x²+2x+3とすると、f'(x)=2x+2=2(x+1)だから、

　　

という公式を用いて、

　　

と、解くこともできる。

なお、

　　

だから、|x²+2x+3|=x²+2x+3である。

 

問題２　次の不定積分を求めよ。

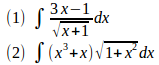
【解】

（１） とおくと

　　

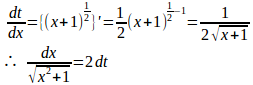
また、t²=x+1より、x=t²−1。

よって

　　

 

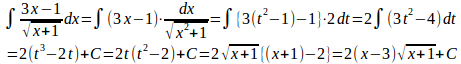
（２）　とおくと

　　

よって、
　　

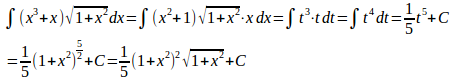
（解答終了）

次のように解いたほうがいいのかもしれない。

【別解】

（１）　とおくと、t²=x+1より、x=t²−1。

よって、

　　

また、3x−1=3t²−4

よって、

　　

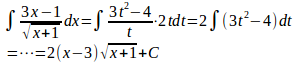
（２）　x²+1=tとおくと

　　

よって、
　　

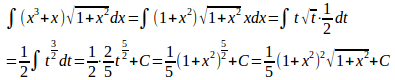
（解答終了）

という不定積分は、t=sinxとおくと

　　

よって

　　

になる。

同様に、t=cosxとおくと

　　

だから

　　

になる。

 

問題３　次の不定積分を求めよ。

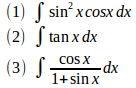
【解】

（１）　sinx= tとおくと

　　

よって
　　

（２）

　　

cosx=tとおくと

　　

よって、

　　

（３）　1+sinx=tとおくと

　　

よって

　　

（解答終了）

（２）、（３）は

　　

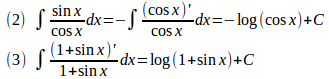
と解いてもよい。

また、

（３）は、sinx=tとおき

　　

と解いてもよい。

 

次に、

　　

というタイプの不定積分は、とおくと

　　

とするとよい。

問題４　次の不定積分を求めよ。

　　

【解】

とおくと
　　
だから、

　　
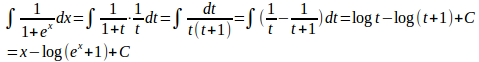
（解答終了）

タグ：微分積分

ワンポイントゼミ１８

ワンポイントゼミ１８

問題　関数F(x)の導関数はx³−3xで、F(0)=2である。

（１）　F(x)を求めよ。

（２）　F(x)の極大値と極小値を求めよ。

（３）　F(x)のグラフの概形をかけ。

【考え方】

（１）　関数F(x)の導関数はx³−3x。

つまり、

　　

したがって、不定積分の定義より

　　

F(0)=2だから、

　　

になり、

　　

（２）　F(x)が求まったので、極値を求めるために、求めたF(x)を微分するというのは、阿⑨の所業。これは問題文に既に

　　

と書いてある。

極値になる点では、F'(x)=0だから、

　　

したがって、極値になる可能性のある点のx座標はx=0、±√3。

極値の判定のために、第２次導関数を求めると、

　　

したがって、x=0のとき極大で極大値はF(0)=2。

x=±√3のとき、極小で、極大値は

　　

と判定することができる。

しかし、基本にかえって、増減表を書くことにする。




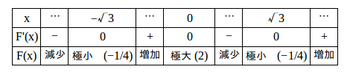
（３）

　　

だから、F(x)はx軸とx=±√2とy=±2で交わる。

また、

　　

だから、F(x)はx=±1で変曲点をもつ。凸凹表を書くと



したがって、グラフの概形は次のとおり。



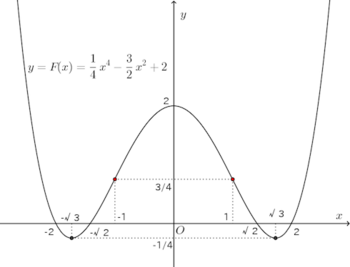
この関数関数F(x)が偶関数、つまり、y軸に関して対称であることを利用すれば、この労力は半分になる。

タグ：微分積分

置換積分１

置換積分１

置換積分

とする。

x=g(t)とおくと、F(x)はtの関数F(g(t))となる。

よって、合成関数の微分より

　　

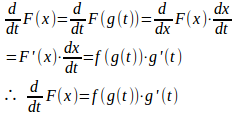
この両辺をｔで積分すると

　　

よって、

　　

これを置換積分法の公式という。

 

例１

　　

【解】

t=1−xとおくと、x=1−t。

よって、

　　

したがって、

　　

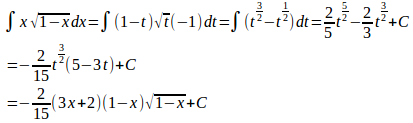
（解答終わり）

問題　次の不定積分を求めよ。

　　

【解】

t=logxとおくと

　　

よって、

　　

（解答終わり）

t=g(x)のときは、①のxとtを入れ換えて、

　　

とし、次のように解くこともできる。

【別解】

t=logxとおき、両辺をxで微分すると

　　

したがって、

　　

（別解おわり）

なのですが、あたかも分数のごとく

　　

や

　　

と、形式的に考えると、何かと便利。

 

例２

　　

【解】

t=x²+1とおき、両辺をxで微分する。

　　

よって

　　

（解答終わり）

（※）

　　

つまり、分数のように

　　

と計算することができる。

 

例３　F'(x)=f(x)のとき、

　　

【解】

t=ax+bとおくと

　　

よって

　　

（解答終わり）

例４

　　

【解】

t=f(x)とおくと

　　

よって

　　

（解答終わり）

ちなみに例２は、例４の特殊なもので、f(x)=x²+1とすれば、例２の結果を得ることができる。

タグ：微分積分

ワンポイントゼミ１７

ワンポイントゼミ１７

これからしばらく積分の計算方法についての記事が続くので、それを補う形で、応用的な問題をワンポイントゼミで解くことにする。

問題　y=f(x)はすべてのxに対し、0<y<1かつを満足し、であるとする。

（１）　f(x)を求めよ。

（２）　を求めよ。

【考え方】

不定積分

　　

を求めるために、まず、被積分関数を部分分数に分解する必要がある。

そこで、まず

　　

として、両辺を比較することによって係数A、Bを求める。

そうすると、

　　

これが0<y<1のすべてのyについて成り立つためには、

　　

これから、A=1、B=−1になり、

　　

よって

　　

したがって、

　　

x=0のときy=2/3だから

　　

よって

　　

（２）のx→∞の極限を求めるにあたって、次のことに注意が必要。

a<0のとき

　　

a=0のときになるので

　　

a>0のとき

　　

したがって、

　　

は、

a<0のとき1

a=0のとき2/3

a>0のとき0

になる。

これをまとめて、解答を作ればよい。

不定積分（数学３）

不定積分（数学３）

§１　不定積分とは

関数f(x)に対して、導関数F'(x)がf(x)に等しい、すなわち、

　　

である関数F(x)を関数f(x)の原始関数または不定積分といい、

　　

であらわす。

また、不定積分を求めることをf(x)を積分するという。

F(x)をf(x)の不定積分の１つ、Cを定数とすると、

　　

だから、F(x)+Cもf(x)の不定積分である。

逆に、f(x)の任意の不定積分をG(x)とすると、

　　

よって、f(x)の不定積分の一つをF(x)、Cを任意の定数とすれば、f(x)のすべての不定積分は

　　

であらわされ、この定数Cを積分定数という。

 

§２　不定積分の基本公式

f(x)、g(x)をそれぞれF(x)、G(x)の導関数とすると、F'(x)=f(x)、G'(x)=g(x)だから、

　　

これより、積分定数Cを省略し

　　

が成立する。

また、

　　

さらに、

　　

指数関数については

　　

三角関数については

　　

§３　簡単な計算問題

問１　次の不定積分を求めよ。

　　

【解】
　　

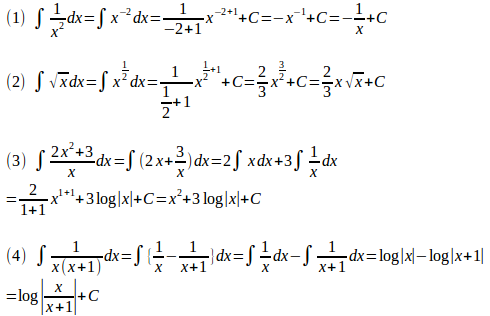
（解答終わり）

この問題の（４）のような分数関数の積分では、一度、部分分数に分解して計算をするとよい。

問題２　次の不定積分を求めよ。

　　

【解】
　　

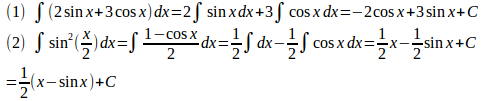
（解答終わり）

（２）では、３角関数の半角公式

　　

が使われている。

タグ：微分積分