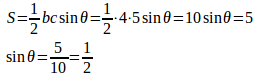第14回 幾何的な問題を・・・ [ネコ騙し数学]
第14回 幾何的な問題を・・・
三角関数の最終回として、その応用として、幾何的な問題を幾つか解いてみることにする。
問題1 acosA=bcosBを満足する△ABCはどのような三角形か。ただし、a=BC、b=CAとする。
【解】余弦定理より

よって、BC=CAの二等辺三角形、または、∠C=90°の直角三角形。
問題2 次の問いに答えよ。
(1) AB=4、AC=3、∠BAC=30°を満足する△ABCがある。この三角形の面積を求めよ。
(2) AB=4、AC=3、∠ABC=30°を満足する△ABCがある。この三角形の面積を求めよ。【解】
(1)
(2) BC=aとする。余弦定理より
問題3 △ABCで
【解】

余弦定理から

よって
問題4 3辺の長さがそれぞれ13、8、7である三角形について次の値を求めよ。
(1) 面積 (2) 最大角 (3) 外接円の半径 (4) 内接円の半径(1) ヘロンの公式は使わないにゃ。
a=13、b=8、c=7とおき、余弦定理を使うケロ!!
よって、
(2) 最大角は120°
(3) 外接円の半径をRとすると、正弦定理より
(4) 内接円の半径をrとすると
(1)では、
さらに、補足すると、最大角は、辺の長さが最も大きい辺に対応する角になる。
ちょっと自慢していいケロか?
この図は正確なんだにゃ。
何と、分度器で測ると、(1)の答え、∠A=120°が出てくるという優れもの(^^ゞ
嘘だと思うなら測ってみろ!!
第13回 問題演習2 [ネコ騙し数学]
第13回 問題演習2
x軸と角度θをなし、原点Oを通過する直線があるとする。
tanの定義は
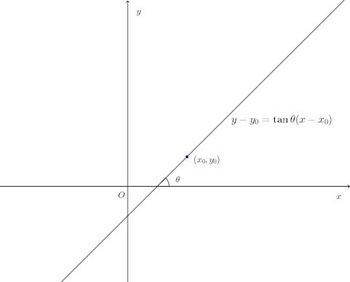
このことから、x軸と角度θをなす、点(x₀,y₀)を通る直線の方程式は
このことを踏まえて、次の問題を解いてみることにする。
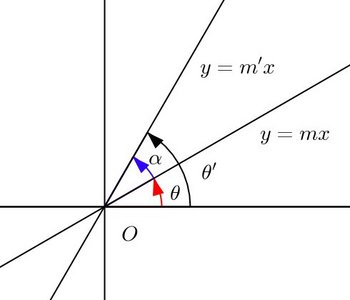
問題1 2直線y=mx+kとy=m'x+k'の作る角(はじめの直線からあとの直線の方へまわる角)をαとする。1+mm'=0のとき
y=mx+k、y=m'x+k'に平行な原点を通る直線は
よって、
ちなみに、1+mm'=0という条件は
また、このとき、①式の分母が0になるので、①式は意味を持たない。
問題2 2直線
【解】
3x−y−2=0はy=3x+2だから、傾きm=3。そして、x−2y+5=0はy=x/2−5/2だから、の傾きm'=1/2。よって、①より
問題3 sin⁴θ+cos⁴θの最大値・最小値を求めよ。
【解】sin²+cos²=1だからcos²θ=1−sin²θ。
さらに、u=sin²θとおくと
u=sin²θだから、0≦u²≦1で
よって、
u=1/2のとき、f(u)は最小で最小値は1/2。u=0、1のとき、f(u)は最大で最大値はf(0)=f(1)=1。
類題
(1) sin⁶θ+cos⁶θの最大値・最小値を求めよ。(2) sin⁸θ+cos⁸θの最大値・最小値を求めよ。
【答】(1) 最小値1/4 最大値1
(2) 最小値1/8 最大値1
問題4
【解】
【別解1】
sinx=u、cosx=vとし
よって、
あるいは、②より
三角関数の合成公式を使う方法が一番自然な解法なのでしょうけれど・・・。
第12回 三角関数の積和・和積の公式 [ネコ騙し数学]
第12回 三角関数の積和・和積の公式
§1 三角関数の積和の公式
三角関数の加法定理より正弦関数については次の関係が成り立つ。よって、①+②は
①−②は
正弦関数と余弦関数の積を正弦関数の和に変えた。
こういうのを、三角関数の積和公式とかいうにゃ。同様に、余弦関数に関する加法定理は
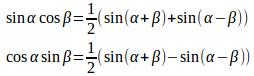
以上の結果をまとめると
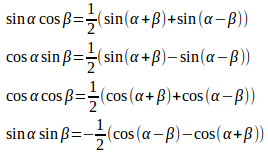
上の式は、積分の計算、たとえば
非常に重要な公式であるのだけれど、私は覚えていない(^^ゞ
こんな式は、加法定理からすぐに導ける。覚える必要はないケロ。さらにいうならば、加法定理も
§2 三角関数の和積の公式
三角関数の積和の公式を導く前、たとえば、
A=α+β、B=α−βとすると、
また、
結果をまとめると、
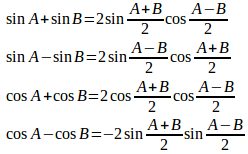
三角関数の和・差から三角関数の積に直すので、和積の公式とか呼んでいるケロ。
上の2番目、4番目の公式は、正弦関数と余弦関数の微分のところで使った。
バズル的な問題を・・・。
問題1 △ABCで
【解】
C=π−(A+B)だから
問題2 α+β+γ=πのとき
加法定理より
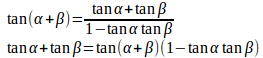
よって、
第11回 合成公式 [ネコ騙し数学]
第11回 合成公式
次の図のようなxy平面上の点があるとする。
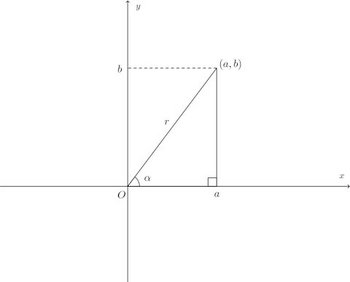
このとき、
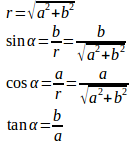
が成立する。
このことは三角関数の定義より明らかでしょう。上で定義した角度αを使うと、asinθ+bcosθは次のように変形できる。
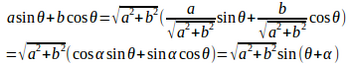
これを三角関数の合成公式という。
あらためて書くと、
そうでないと、aとb、どっちが分母で分子かで悩むことになる。
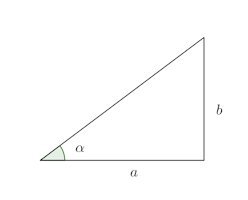
例1 sinθ+cosθは、a=b=1の場合で
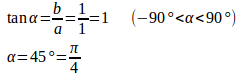
とすると、
例2 3sinx+4cosx(0≦x<2π)の最大値、最小値を求めよ。
【解】
問題 x²+y²=1のとき、x+yの取りうる値の範囲を求めよ。
【解】
x=cosθ、y=sinθ(0≦θ<2π)とする。
ちなみに、x+yが最大になるとき、
【別解】
シュワルツの不等式
【別解2】
x+y=kとする。y=k−xをx²+y²=1に代入する。
この他にも別解はいくつか作れますが、別解2は好きじゃない。これは自然な考え方ではないケロ。
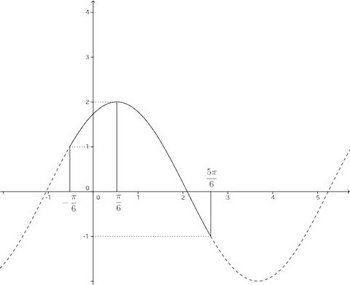
x+y=kとし、これを直線の方程式とみなし、原点を中心とする半径1の円x²+y²=1との共有点を調べる図形的に解く方法もある。
次の図のように接する時に最大・最小になる。そして、y軸の赤い線で示した範囲がx²+y²=1のときx+y=kが取りうる範囲となる。
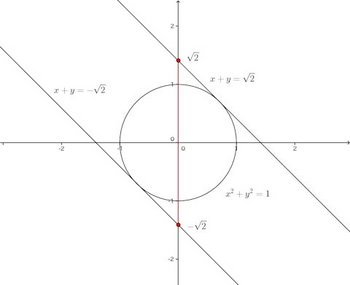
この解法は、もっと嫌いだ!!
問題2
問題3
(1) t=sinx+cosxとおき、tの範囲を定めよ。
(2) f(x)をtの式であらわせ。(3) f(x)の最小値とその時のxの値を求めよ。
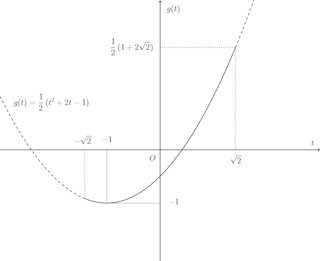
【解】(1) −√2≦t≦√2
(2) t=sinx+cosxを2乗する。
(3)
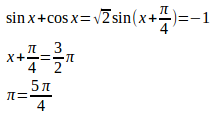
第10回 三角関数の演習問題 [ネコ騙し数学]
第10回 三角関数の演習問題
問題1 cosx+cosy=a、sinx+siny=bのとき、cos(x−y)をa、bを用いてあらわせ。
【解】
上の式と下の式を足すと
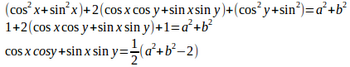
よって、
類題 sinz=cosx+cosy、cosz=sinx+sinyのとき
2cos(x−y)+1=0であることを示せ。
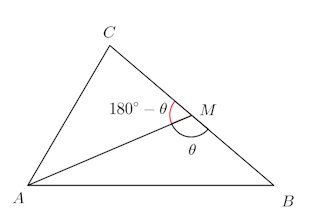
問題2 △ABCの面積S、辺BCの長さをaとするとき、
【解】
△ABCの面積S
余弦定理より
(1)と(2)を比較すると
問題3 半径の円に内接する△ABCの面積が1で
【解】
三角形だから
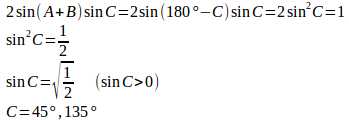
正弦定理より
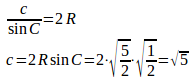
三角形の面積は1だから
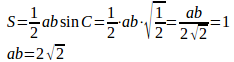
余弦定理より
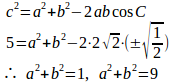
よって、
格好良く解きたい人は
すると、
何を書いてあるかわからない人は、真面目に連立方程式を解けばいい!!
問題4 2次方程式
【解】
2次方程式
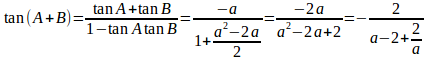
a>0だから相加平均≧相乗平均が使えて
よって、
2次方程式の判別式、解と係数の関係、相加平均≧相乗平均、三角関数の加法定理が組み合わさったいい総合問題だと思うけれど、試験会場で受験生にこれを解けというのは酷だと思うにゃ。
ここで使っている手法を用いると、これまでに何度も出てきた
この関数は、f(−x)=−f(x)が成り立つので、x≧0だけを調べればいい。そして、f(0)=0なので、x>0として
よって、0≦xのとき
となる。
第9回 三角関数の加法定理 [ネコ騙し数学]
第9回 三角関数の加法定理
§1 加法定理
前回の第8回で加法定理を証明したのだけれど、三角形限定の証明なので、より一般的な証明を与えることにする。
行列と一次変換(回転)を用いて証明する証明が一般的なのですが、ねこ騙し数学では行列や一次変換をまだ正式にやっていないので、ベクトルの内積を用いた証明を紹介。
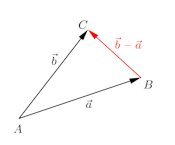
上図のように、単位円(半径1の円)周上に2点、A、Bがあり、線分OA、OBがx軸と角度α、βをなしているとする。このとき、

さらに、
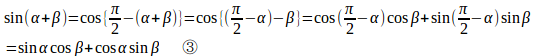
この③を使って
この結果をまとめると、

問題1 次の値を求めよ。
(1) sin75°、cos75°、tan75° (2) sin15°、cos15 °、tan15°
【解】(1) α=45°、β=35°として、加法定理を使うにゃ。
tan30°、tan45°を求めて、さらに加法定理で計算するなんて、阿呆のやることだにゃ(^^ゞ
公式を憶えているから、そんな阿呆な解法を思いつく。(2) α=60°、β=45°やα=45°、β=30°として、sin(α−β)=sinαcosβ−sinβcosαを使えば・・・。
【答】
(1)の答えと似ているが、これは偶然、必然(・・?
15°=90°−75°ではある。
問題2
【解】
sinα=1/2のとき、αは鋭角なのでcosα>0
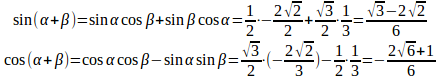
sinα=1/2で、αは鋭角なので、α=30°。よって、
§2 倍角公式と半角公式
に対して、α=βとすると、
これを三角関数の倍角公式という。
cosの倍角公式に注目すると、
θ=2αとすると、上の式は

となる。この式を半角公式と呼ぶ。
この半角公式を用いると、問題1(2)のsin15°、cos15°は、θ=30°として

と求めることができる。
問題1の(2)と値が違うように見えますが、これは同じ値だケロ!!
問題3 k=tanxとすると、
【解】
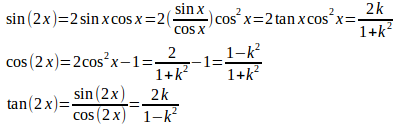
上の解答では
第8回 加法定理と中線定理 [ネコ騙し数学]
第8回 加法定理と中線定理
問題1 加法定理
(1) △ABCにおいて
(2) (1)の結果を用いて、
【解】
(1) 第1余弦定理
(2)
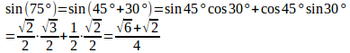
(解答終わり)
あくまで形式的な議論だけれど、
さらに、
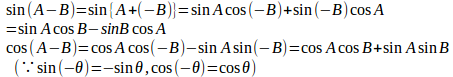
となり、
(1)で、第1余弦定理を使っているけれど、これは次の図を見れば第1余弦定理を覚えていなくても、その場で導くことができる。
問題2 中線定理
余弦定理を用いて中線定理
よって、
![]()
問題3 (公式?)
△ABCにおいて、1辺の長さaとその両端の角B、Cが与えられているとき、三角形の面積Sは
第7回 三角形の面積 [ネコ騙し数学]
第7回 三角形の面積
△ABCの面積Sは
である。
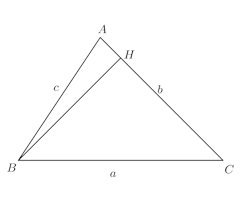
このことは、次の図を見てもらえるとわかると思う。
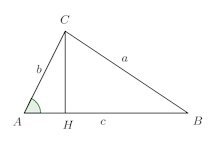
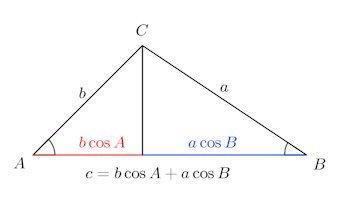
点Cから線分ABに垂線をおろし、垂線の足(交点)をHとし、△AHCに注目すれば、
になるので、
となるし、△CHBに注目すれば、
となる。
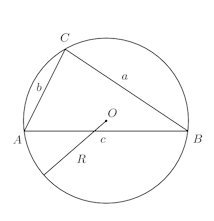
また、△ABCの外接円をRとすれば、正弦定理
を使えば、三角形の三辺の長さと外接円の半径Rを使って
△ABCに内接する円があるとする。内接円の半径をrとする。
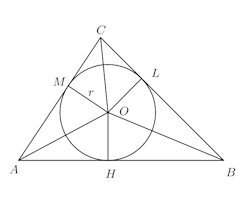
上図を見ると、△ABOの面積S₁は
つまり、三角形の面積は、三角形の三辺の長さの和と内接円の半径をかけたものを半分である
問題1 △ABCにおいて、b=4、c=5、面積5のとき、2辺b、cのなす角と辺aの長さを求めよ。
【解】
b、cのなす角度をθとすると、ここで、「わ〜い、θ=30°だ」と喜ぶと、地獄を見るにゃ。
正弦関数の角関係から
θ=90°の時以外は2つあるケロ。注意が必要だにゃ。
θ=30°のとき、余弦定理を使ってaの長さを求める。
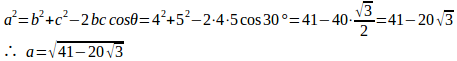
θ=150°のとき
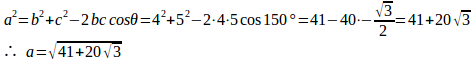
問題2 半径rに内接する正三角形の面積を求めよ。
【解】
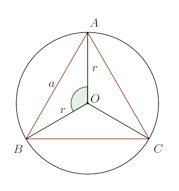
正三角形なので中心角∠AOB=120°。
よって、△AOBの面積は
ちなみに、
【別解】
①を使うならば、次のようにやればよい。
正三角形の一辺の長さをa、面積をSとする。①より、
問題3 四辺形の対角線の長さをa、b、それとなす角をθとすれば、この四辺形の面積Sは
で与えられることを証明せよ。
【解】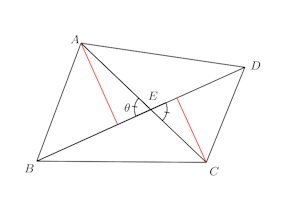
△ABEに注目する。この三角形の高さは
よって
![]()
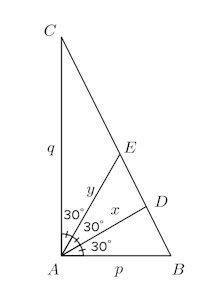
問題4 直角三角形ABCの直角Aの3等分線が斜辺BCと交わる点を、Bの方から順にD、Eとして、AB=p、AD=x、AE=y、AC=qとする。
(1) 三角形の面積を利用して
(2) p=1、q=2のとき、x、yの値を求めよ。
【解】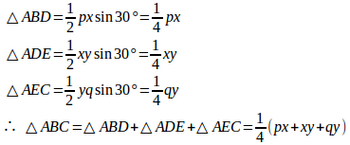
また、
(2) p=1、q=2だから
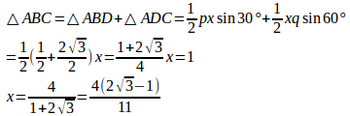
また、
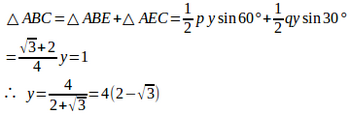
(1)の結果を使えというのかもしれないけれど、コッチのほうが楽でしょう。
第6回 正弦定理 [ネコ騙し数学]
第6回 正弦定理
正弦定理を紹介する前に、その前提となる円周角の定理を紹介。
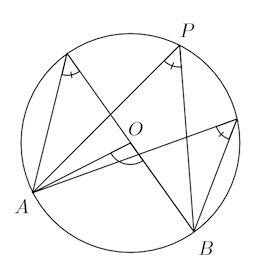
§0 円周角の定理
円周角とは、円周上の1点から、これとは異なる同一円周上の2点に線分を引き、この2つの線分のなす角のことである。
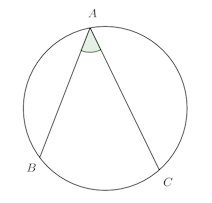
上の図の∠CABが円周角。
円周角の定理
円周角はその弧に対する円周角の半分に等しい。
この定理の証明はしない。これを前提として議論を進めることにする。
さらに、円周角の定理から出てくるのだけれど、半円の円周角は直角90°であることも前提として話を進めるにゃ。§1 正弦定理
正弦定理
△ABCの外接円の半径をRとするとき、である。
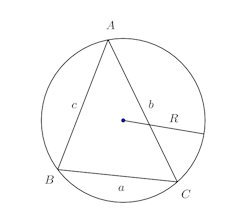
【証明】
Cと円の中心Oを通る直線と円の交点をA’とする。円周角の定理より、∠A=∠A’で、かつ、∠A'BC=∠R。
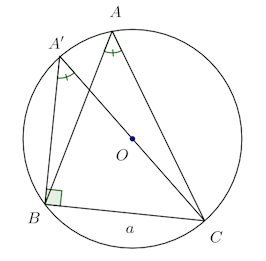
ゆえに、
同様に、各辺に対して行えば
∠Aが鋭角ならばこれで証明終わりだけれど、例によって、直角、鈍角の場合も証明しなければならない。
直角の場合は、∠A'=∠Rの時だからいいでしょう。なので、鈍角の証明をするにゃ。
弦BCに関してAとは反対側の円周上に点Dをとる。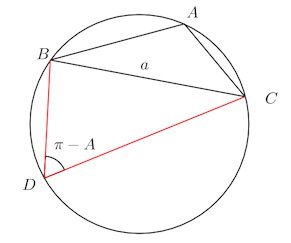
四角形ABDCは円に内接するので、
△BDCに関しては
で、三角関数の角関係を使うと
(証明終わり)
問題1 △ABCについて、次のものを求めよ。
a=10、b=10√3、A=30°のとき、cとBとCを求めよ。【解】
正弦定理より
正弦定理より
C=30°=Aになるので、c=a=10として出してもいいにゃ。
チョット先取りになるけれど、△ABCの面積Sは
問題2 △ABCにおいて、A:B:C=2:3:7、b=10のとき、△ABCの外接円の面積を求めよ。
【解】A:B:C=2:3:7より、B=45°。
外接円の半径をRとすると
何故、Bが45°になるかというと、
問題3 次の等式を満たすとき、△ABCどんな三角形か。
正弦定理より
(2) 代入すると、
第5回 余弦定理 [ネコ騙し数学]
第5回 余弦定理
余弦定理には、第1余弦定理、第2余弦定理の2つがある。そして、一般に余弦定理と呼ばれているものは、第2余弦定理だケロ。
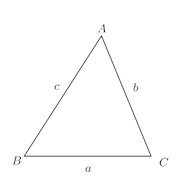
第1余弦定理
第2余弦定理
§1 第1余弦定理
第1余弦定理を証明するにゃ。
【証明】Aから線分BCに垂線をおろし、その垂線の足をHとする。
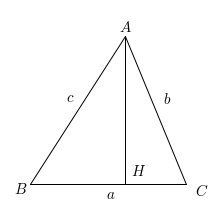
この時、
よって、
b、cについても同様。
(証明終わり)
なのですが、次のような∠Bが鈍角の鈍角三角形の場合もある。
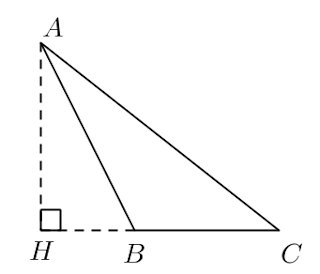
このときは、
鋭角三角形、直角三角形、鈍角三角形であろうが、いずれにせよ、成り立つというわけです。
この定理は、実は、意外に使い道がない(^^ゞ
§2 第2余弦定理
【証明】
点Bから線分CAに垂線をおろし、その垂線の足をHとする。
そして、三角比より
(証明終わり)
ここでも、先の第1余弦定理の証明と同じように、鋭角、直角、鈍角三角形に分けて証明しないといけないけれど、面倒なのでしないにゃ。
これは循環論法で証明になっていないという話もあるが(^^ゞ
気が向いたら、証明を付け足すにゃ。
余弦定理から三角形の三辺の長さが与えられていると、次のように角度を求めることができる。
非常に美しい式の形をしているので、この式が好きだというヒトは結構いるにゃ。
問題 △ABCにおいて、BC=4、CA=5、AB=6のとき、
(1) cosBを求めよ。
(2) sinBを求めよ。
(4) 辺AB上の点EをAE=4となるようにとったとき、CEの長さを求めよ。
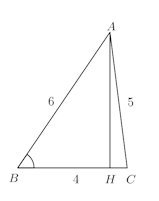
【解】
(1) a=BC==4、b=CA=5、c=AB=6とすると、余弦定理より
(2) sin²B+cos²B=1だから
(3) AH=AB×sinBだから
(4) △BCEに対して余弦定理を用いると
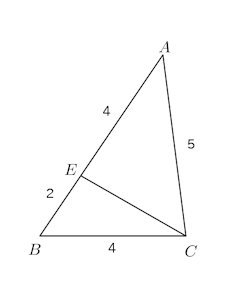
実は、(1)、(2)は、ヒントとなるように付け足した小問なんだけれど、余弦定理の使い方がよくわかるいい問題だと思う。
(3)、(4)は、三平方の定理と2次方程式を用いれば、余弦定理を使わなくても解けることは解けるけれど、計算が大変だケロよ。