第4回 三角関数の角関係 [ネコ騙し数学]
第4回 三角関数の角関係
§1 三角関数の角関係
三角関数には、角関係と呼ばれる次のようなものあります。
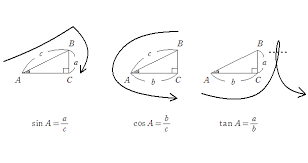
(1)の関係については、この図を見れば、何故こうなるのか、わかると思うにゃ。
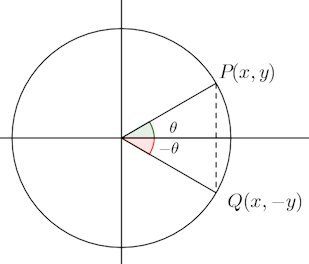
(2)は、次の図を見ればわかると思うにゃ。
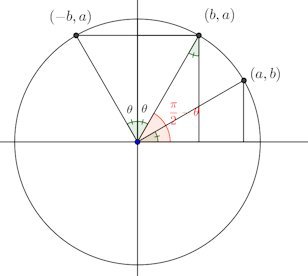
なのですが、
(3)は、次の図から、何故こうなるか、わかると思うにゃ。
三角関数の角関係については、お絵描きにまさるものはない。そして、繰り返し言っていますが、これらの公式は絶対に覚えてはいけない。覚えると、絶対に忘れるにゃ。忘れるだけでなく、覚え間違いをしているかもしれない。
とにかく、お絵描き。そして、sinθは、単位円のx座標の成分、cosθはy座標の成分という基本さえ掴んでおけば、間違えることはない。
§2 問題
問題1 次の不等式を同時に満たす角度θは何象限か。
(1) sinθ<0、cosθ>0 (2) cosθ<0、tanθ>0【解】
単位円(半径1の円)上の点P(x,y)とする。そうすると、x=cosθ、y=sinθ。
(1) x=cosθ<0、y=sinθ>0。よって、第2象限。
(2)
また、x=cosθ<0より、y<0。
よって、x<0、y<0となり、第3象限。問題2 θは第3象限の角であり、
【解】
よって、
問題3 0≦θ≦π/2のとき、
【解】
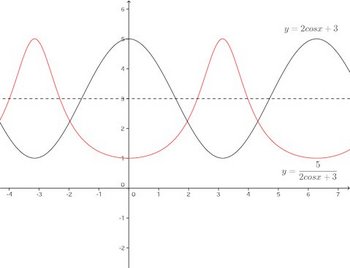
グラフを書くと次のようになる。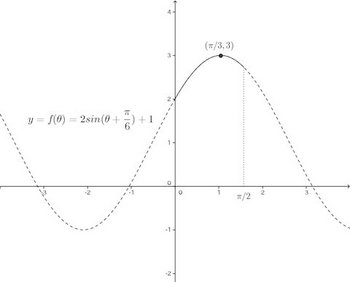
よって、θ=π/3のとき最大で最大値は3、θ=0のとき最小で最小値は2。
ちなみに、このグラフは、
問題4 次の関数の最大値と最小値を求めよ。
(1) −1≦cosx≦1だから、yはcosx=−1のとき最小で最小値は1、cosx=1のとき最大で最大値は5。
(2) 答えだけ。最大値は5、最小値は1。(1)の結果を使えば、こうなるにゃ。問題5 次の方程式を満たす角θを求めよ。
(1)
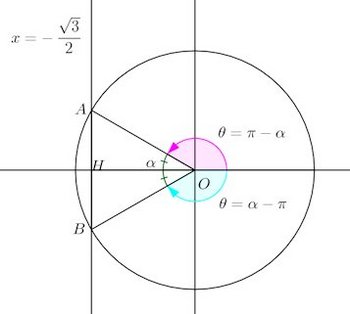
単位円なのでcosθは点Hだにゃ。直角三角形OAHで考えると、OH=√3/2だから、α=30°=π/6だにゃ。
ということで、
なので、一般角は
をみて、θ=150°=5π/6という数字が頭の中に浮かぶヒトはこんな面倒なことをする必要はないけれど、θ=−5π/6が解であることを見落としたりするので、頭の中でこの図をイメージしたほうがいいと思うにゃ。
(2)
−π/2<2θ<π/2の範囲でtan(2θ)=√3になるのは、2θ=60°=π/3(rad)のとき。tanは周期πだから、一般角はこの値にnπをつけないといけない。
(3)
第3回 三角関数 [ネコ騙し数学]
第3回 三角関数
§1 円と扇型(小・中学の復習)
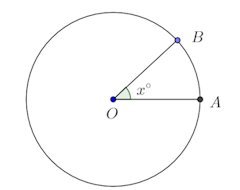
上の図に示すような半径rの円と、中心角をx°とするその扇型があるとする。
このとき、円弧ABの長さlは次のような簡単な比例関係
また、同様な比例計算から扇型の面積Sは
§2 弧度法
(1)、(2)を見ればわかるけれど、この180°や360°という定数が邪魔で何とも目障りだにゃ。円周率πも定数だし、そこで、
度数法から弧度法への角度の変換式は(a)で与えられるのだけれど、180°がπ(rad)なので、
数学(の問題)でよく出てくるのは、
180°がπ(rad)だから、覚える必要もないもないけれど・・・。
§3 三角関数
三角比は直角三角形の辺の比で次のように定義される。
これでは何かと不便なので、三角比を元に三角関数を次のように定義するにゃ。
原点を中心とする半径rの円周上の点Pのx座標、y座標をx、yとし、さらに、線分OPとx軸となす角度をθ(半時計回りが正、時計回りは負)とする。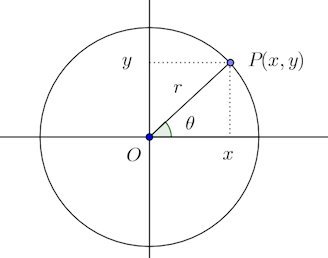
このように定義すれば、三角比の角度の制限がなくなり、θを実数全体に拡張できるにゃ。
そして、このように定義された関数を三角関数と言う。r=1、つまり、原点を中心とする単位円の場合、三角関数の定義は簡単になり
どちらで三角関数を定義しても構わないにゃ。
ところで、円周上の点Pに対して
また、
さらに、sin²θ+cos²θ=1の両辺をcos²sθで割ると、
§3 三角関数のグラフ
y=sinx、y=cosxのグラフを書くと次のようになる。xは弧度法の角度で単位はrad。
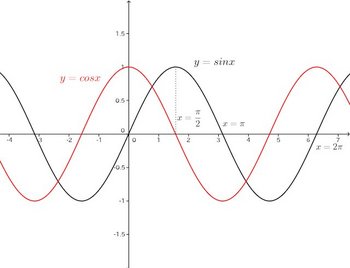
この図を見るとわかるけれど、sinxとcosxともに2πという周期をもつ周期関数で、当たり前といえば当たり前だけれど、
tanxをグラフにすると、次のようになる。
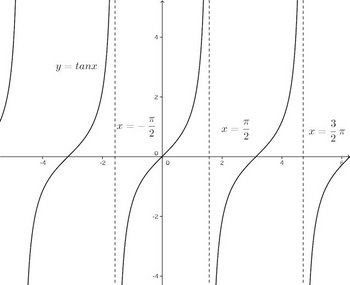
この関数は定義からわかると思うけれど、分母である余弦関数cosxが0になるところ、つまり、cosx=0で不連続になる。そして、周期はπだにゃ。
§4 一般角
複素関数のところでも少し話したけれど、角度は一意じゃ〜ない。
度数法で書くと、角度α°とぐるりと一周した角度α°+360°、さらにn周した角度α°+360°nと区別することができない。ということで、
弧度法だと一般角は
第2回 三角比2 [ネコ騙し数学]
第2回 三角比2
前回やった三角比の応用として、三角比を使って幾何的な問題をいくつか解くことにするにゃ。
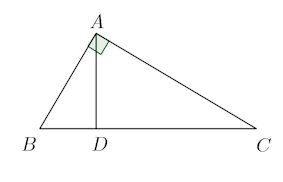
問題1 A=∠R(直角)の直角三角形ABCにおいて、頂点Aから斜辺BCにおろした垂線の足をDとするとき、ADを辺BC(=a)と∠Cであらわせ。
△ABCで
①を②に代入して、
【別解】
△ABCで
問題2 下の図を用いて、tan22.5°、tan67.5°を求めよ。
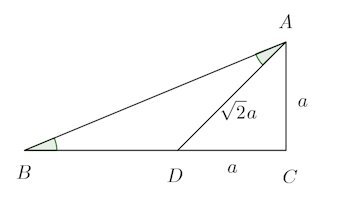
【解】
線分BC上に、∠ABC=∠DAB=22.5°となるような点Dをとる。そうすると、三角形ABDはBD=DAの二等辺三角形になる。
このとき、∠ADB=45°になり、三角形ADCはDC=CA=aの直角二等辺三角形。三平方の定理を使うと、ADの長さは
問題にはないけれど、三角形ABCは直角三角形なので、三平方の定理が成り立ち、
また、前回やった
この計算をして、同じ値になることを確かめて欲しいにゃ。
問題3 次の図のように、観測者の目の点Eから木の頂上を見上げたら、∠AEC=45°、また点Eから木の根元Bを見下ろしたら、∠CEB=30°で、EからBまでの距離は3mであった。木の高さBAを求めよ。
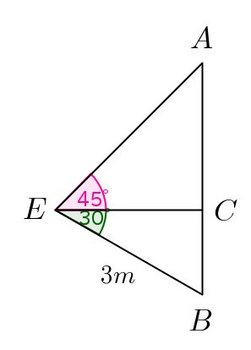
【解】
△EBCに注目!!
また、
【別解】
頭は飾りじゃないケロよ。少しは頭を使うべきだと思うケロ。
第1回 三角比1 [ネコ騙し数学]
第1回 三角比1
これまで、三角関数についての話はしてきたけれど、三角関数のベースになる三角比についてはやって来なかったので、今回、その話をすることにするにゃ。
下に示すような、∠C=90°、AB=c、BC=a、CA=bの直角三角形があるとする。
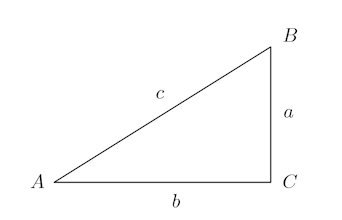
このとき、三角比は次のように定義される。
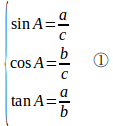
△ABCは∠C=90°の直角三角形なので、三平方の定理(ピタゴラスの定理)が成立する。
この導出過程を見れば明らかなように、②は三平方の定理⑨と同等で、三平方の定理を三角比で書き直したものである。
②を辺の長さであらわし直せば、
また、
さらに、cosA≠0のとき、②の両辺をcos²Aで割ると、
ということで、早速問題を解いてみることにする。
問題1 cosA=0.8のとき、sinA、tanAの値を求めよ。
【解】sinAとcosAの間には、
よって、
小数のままだと気づきにくいと思うのだけれど、これは、中学校で習った、辺の長さの比、a:b:c=3:4:5の直角三角形なんだケロ。
ちなみに、tanAは④を使っても求まるケロ。
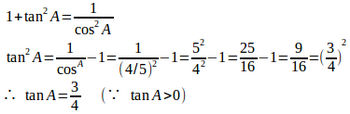
今やっているのは、三角関数ではなく、(直角三角形の)三角比だケロ。これは直角三角形の辺の長さの比だから、三角関数とは違って、0や負の値になることはないにゃ。正の値しかとりえないにゃ。
さらに、もう一問。
問題2 次の等式を証明せよ。
ところで、直角三角形△ABCを次のように置くにゃ。
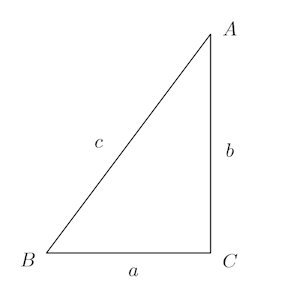
そうすると、
また、A+B=90°だから、B=90°−Aとなり、
あと、三角比で知っておくことは、
A=45°のとき、直角三角形ABCは直角二等辺三角形になるのだから、
30°の場合は、一辺の長さがaの正三角形ABCの頂点AからBCに垂線をおろし、BCとの交点をHとする。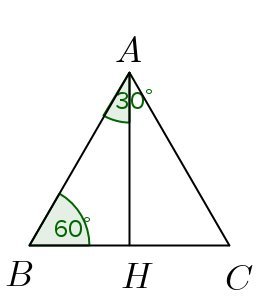
要するに、
ちなみに、三角比の覚え方としては、次のものがあります。これで覚えるのが一番てっとり早くて安全です。。