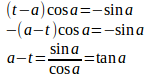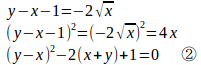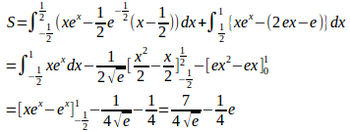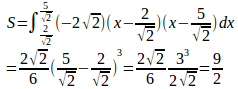定積分の応用 面積の分割に関する問題 [ネコ騙し数学]
定積分の応用 面積の分割に関する問題
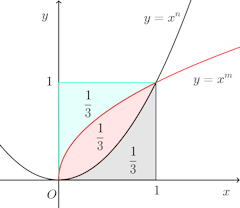
問題1 直交軸において、原点と点(1,1)を結ぶ線分を対角線とする正方形がある。方程式において、nを変えると種々の曲線ができるが、その中から2つの曲線を求めて、これによって正方形を3等分せよ。
 【解】
【解】3等分する2つの曲線を
(解答終了)
点(1,1)を点Aとし、原点OとAとを直線で結ぶと、直線OA、つまりy=xに関して対称。
y=x²の定義域を0≦x≦1とすれば、もう一方の曲線はx=y²(0≦y≦1)で、これからy=√xが出てくる。
問題2 aを正の定数とするとき、曲線
【解】
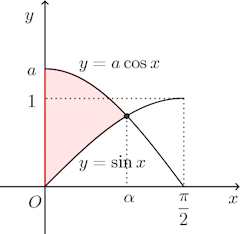 0<x<π/2におけるy=acosxとy=sinxの交点のx座標をαとすると、
0<x<π/2におけるy=acosxとy=sinxの交点のx座標をαとすると、
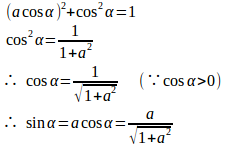
問題の条件より
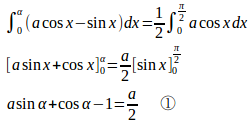
①に
を代入すると、
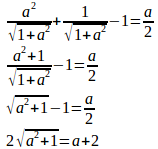
両辺を2乗すると、
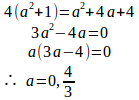
a>0だから、
問題3 曲線y=sinx上の点P(a,b)における接線とx軸との交点をKとし、Pからx軸におろした垂線の足をHとする。
△PKHが曲線y=sinxによって分けられる2つの部分の面積比が(図形PKO):(図形POH)=1:2
となるようにaを定めよ。ただし、Oは座標の原点、0<a<π/2とする。【解】
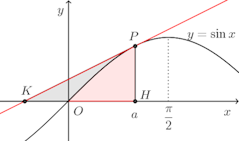 図形PKO:図形POH=1:2だから、
図形PKO:図形POH=1:2だから、△PKH:図形POH=3:2
接点Pにおける接線の方程式は、y'=cosxだからこの接線とx軸との交点Kのx座標をtとすると
よって、△PKHの面積S₁は
よって、①と②より
問題4 曲線y=logxとx軸との交点をAとする。また、この曲線に原点Oから引いた接線の接点をB、Bからx軸におろした垂線の足をHとする。
(1) 接線OBの方程式を求めよ。(2) 線分AH上に1点Pをとり、線分AP、BPおよび曲線ABの囲む面積を△BOHの半分にしたい。Pのx座標を求めよ。
【解】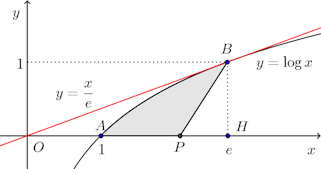 (1) 接点Bの座標を(t,logt)とすると、y'=1/xだから、接線の方程式は
(1) 接点Bの座標を(t,logt)とすると、y'=1/xだから、接線の方程式は
(2) 接点Bの座標は(e,1)だから、△BOHの面積は
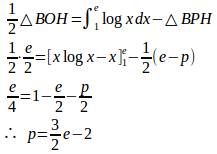
(解答終了)
ネムネコ、閃く!!というほどのものではないが… [ネコ騙し数学]
ネムネコ、閃く!!というほどのものではないが…
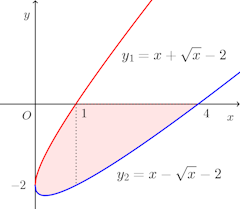
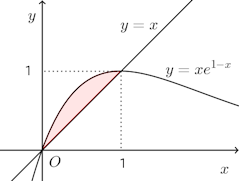
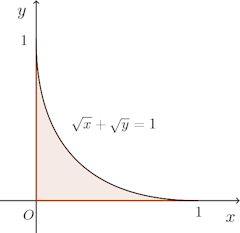 問題 次の曲線とx軸、y軸の間で囲まれる部分の面積を求めよ。
問題 次の曲線とx軸、y軸の間で囲まれる部分の面積を求めよ。
根号内で負になってはいけないので、x≧0、y≧0。
また、
したがって、0≦x≦1、0≦y≦1
また、
なのですが、
したがって、次のように解くこともできる。
【別解】
曲線①は媒介変数を用いて
別解は、問題の解答中に出てくる定積分
また、
だから、
ここで、
つまり、曲線①の正体は放物線の一部ということが分かる。
接線と面積 [ネコ騙し数学]
接線と面積
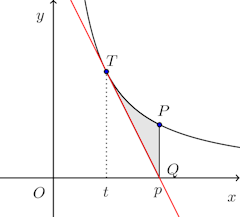
問題1 直角双曲線xy=k(k>0)の上の1点Pからx軸におろした垂線の足をQ、Qからこの双曲線に引いた接線の接点をTとすると、線分PQ、および双曲線の弧TPで囲まれる部分の面積Sは、Pが双曲線のっどこにあっても一定であることを示せ。
【解】接点Tの座標をとすると、
だから、接線の方程式は
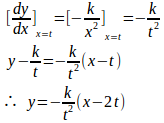
点Q(p,0)を通るので
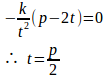
よって、接線の方程式は
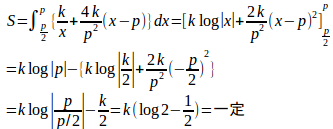
(解答終了)
問題2 曲線上の点P
における接線とx軸の交点をQとする。P、Qからy軸に平行に引いた直線と、上の曲線およびx軸とで囲まれた部分は、PQによってどのような比に分けられるか。
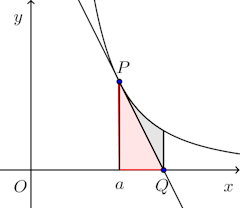
は偶関数で、x軸に関して対称なので、a>0について考えれば十分。
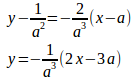
よって、x軸との交点Qのx座標は
したがって、面積比は
問題3
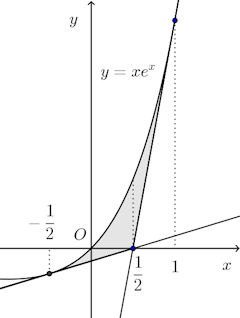
(1) x軸上の点P(a,0)から曲線に2本の接線が引けるためのaの条件を求めよ。
(2) a=1/2のとき、この曲線と上の2接線で囲まれる部分の面積を求めよ。
【解】
接点の座標をとすると、接線の方程式は
(2) a=1/2のとき
(解答終了)
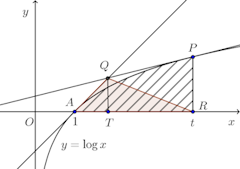
問題4 曲線y=logx上の定点A(1,0)と動点Pとにおける接線の交点をQとする。またP、Qからx軸へおろした垂線の足をそれぞれR、Tとし、この曲線とPR、ARによって囲まれた部分の曲線をSを、△AQRの面積S₁、△APTの面積をS₂とする。
(1) の値を求めよ。
(2) Pがこの曲線に沿ってAに近づくの極限値を求めよ。
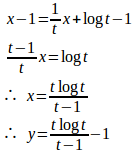
よって、
③と④より、
定積分の応用 閉曲線の面積 [ネコ騙し数学]
接線と面積
問題1 直角双曲線xy=k(k>0)の上の1点Pからx軸におろした垂線の足をQ、Qからこの双曲線に引いた接線の接点をTとすると、線分PQ、および双曲線の弧TPで囲まれる部分の面積Sは、Pが双曲線のっどこにあっても一定であることを示せ。
【解】接点Tの座標をとすると、
だから、接線の方程式は
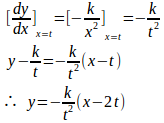
点Q(p,0)を通るので
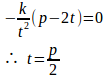
よって、接線の方程式は
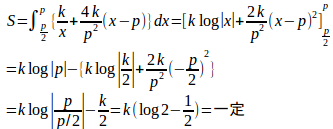
(解答終了)
問題2 曲線上の点P
における接線とx軸の交点をQとする。P、Qからy軸に平行に引いた直線と、上の曲線およびx軸とで囲まれた部分は、PQによってどのような比に分けられるか。

は偶関数で、x軸に関して対称なので、a>0について考えれば十分。
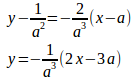
よって、x軸との交点Qのx座標は
したがって、面積比は
問題3
(1) x軸上の点P(a,0)から曲線に2本の接線が引けるためのaの条件を求めよ。
(2) a=1/2のとき、この曲線と上の2接線で囲まれる部分の面積を求めよ。
【解】
接点の座標をとすると、接線の方程式は
(2) a=1/2のとき
(解答終了)
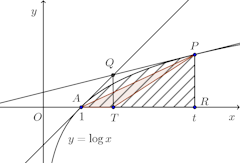
問題4 曲線y=logx上の定点A(1,0)と動点Pとにおける接線の交点をQとする。またP、Qからx軸へおろした垂線の足をそれぞれR、Tとし、この曲線とPR、ARによって囲まれた部分の曲線をSを、△AQRの面積S₁、△APTの面積をS₂とする。
(1) の値を求めよ。
(2) Pがこの曲線に沿ってAに近づくの極限値を求めよ。
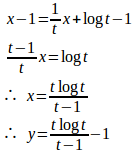
よって、
③と④より、
![]()
ワンポイントゼミ x=t²+1、y=2−t−t²のグラフならび・・・ [ネコ騙し数学]
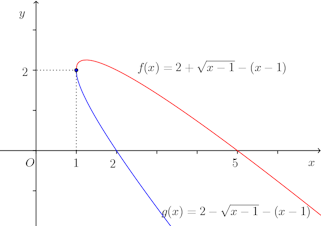
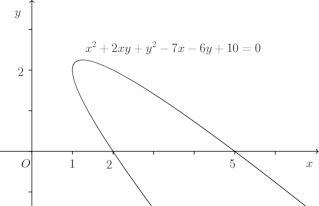
ワンポイントゼミ x=t²+1、y=2−t−t²のグラフならび・・・
ここから先は読むな!!
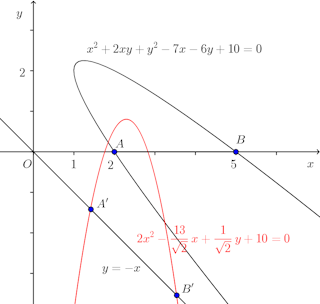 この曲線の正体は、原点を中心に45°時計回りに回転させるとわかります。
この曲線の正体は、原点を中心に45°時計回りに回転させるとわかります。
このとき、x軸はy=−xに写されるので、放物線
点A(2,0)、点B(5,0)の像A'、B'のx座標はそれぞれ2/√2、5/√2になるので、
放物線の定積分に関する次の公式
を用いると、と求められる。
ちなみに、点(x,y)を原点を中心に半時計回りにθ回転して得られる点(x',y')は、行列を用いて書くと
あなた、読むなと言ったのに、読みましたね。
頭が呪われたにゃ!!
定積分の応用 面積4 媒介変数で表された曲線の場合2 [ネコ騙し数学]
定積分の応用 面積4 媒介変数で表された曲線の場合2
前回に引き続き、媒介変数で表された曲線の面積を求める問題を解くことにする。
前回解いた問題は、どれも、a≦x≦bにおいてdx/dt≧0、または、dx/dt≦0、つまり、xがtに関して(広義の)単調増加、または、単調減少の場合で、今回はより複雑なdx/dtの符合が正から負、または、負から正に変わるより複雑なものを扱うことにする。
問題1 曲線x=3t−t³、y=4−t⁴(−√2≦t≦√2)とx軸で囲まれた部分の面積を求めよ。
【解き方】
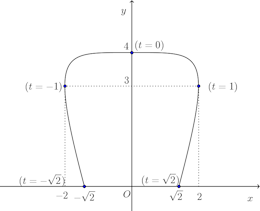 この曲線とx軸との交点のtの値は、y=0から
この曲線とx軸との交点のtの値は、y=0から
したがって、求めるべき面積は第1象限の部分(0≧t≦√2)の面積の2倍である。
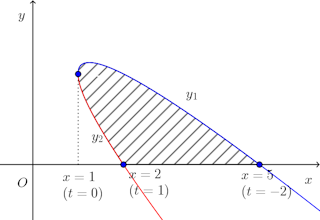
そこで、この曲線の0≦t≦1の部分をy₁、この曲線の1≦t≦√2の部分をy₂とおくと、右の図になる。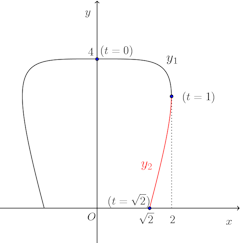 だから、曲線y₁、y₂、そして、x軸、y軸で囲まれた部分の面積は
だから、曲線y₁、y₂、そして、x軸、y軸で囲まれた部分の面積は
注意すべことは、0≦t≦√2のとき
そして、x=√2に対応するtはt=√2、x=2に対応するtはt=1であること。
だから、
また、
さらに、①をxで微分すると
意欲のある人は、
問題2 次の方程式のあらわす曲線とx軸とで囲まれた部分の面積を求めよ。
そして、
【解】
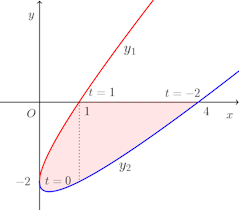 y=t²+t−2とx軸との交点のtの値を
y=t²+t−2とx軸との交点のtの値を
0<t≦1でxは増加し、t=0のときx=0、t=1のときx=1。
0≦t≦1の曲線の部分をy₁、−2≦t≦0の曲線をy₂とすると、したがって、面積Sは
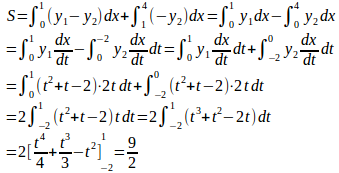
(解答終了)
問題3 tがすべての実数の範囲を動くとき、
【略解】
なお、問題1、2、3では、
という定積分の性質を使っている。
定積分の応用 面積3 曲線が媒介変数で表された場合 [ネコ騙し数学]
定積分の応用 面積3 曲線が媒介変数で表された場合
曲線がパラメータで表された場合
次のようにパラメータ・媒介変数で表された曲線
特に、a≦x≦bにおいて、y≧0のとき
問題1 サイクロイド
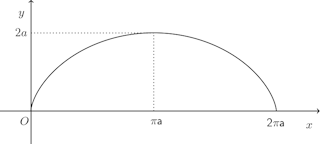
【解】
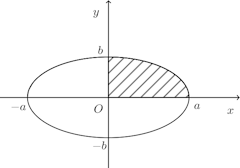
問題2 次の点(x,y)のえがく曲線の囲む図形の面積を求めよ。ただし、a>0、b>0とする。
x=のときθ=π/2、x=aのときθ=0。
よって、
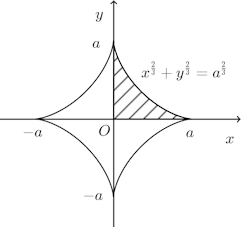
(2) この曲線は
この曲線で囲まれる面積は第1象限の部分を4倍したものに等しい。
上の計算では次の公式を使っている。
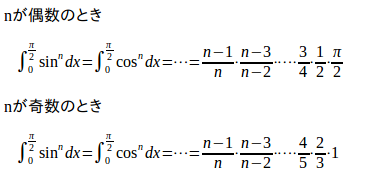
この公式の証明は定積分の漸化式のところで証明をしてある!!
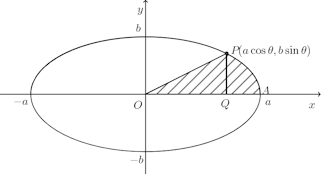
問題3 楕円
弧AP上の点の座標を
求める面積Sは
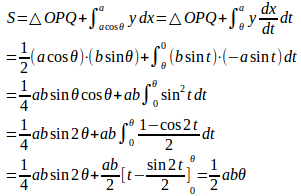
(解答終了)
定積分の応用 面積2 [ネコ騙し数学]
定積分の応用 面積2
問題1 次の図形の面積を求めよ。
(1) 曲線のx軸より下の部分とx軸とで囲まれた図形
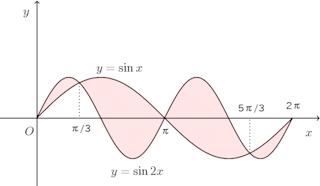
(2) 0≦x≦2πの範囲で、2曲線y=sinxとy=sin2xとで囲まれた部分
【解】
(1) y=cosx(1+sinx)とx軸との交点のx座標はπ/2と3π/2。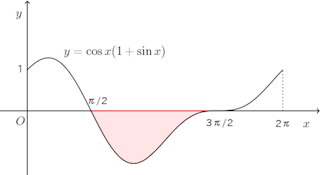
よって、求める面積Sは
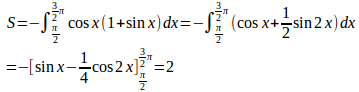
(2) y=sinxとy=sin2xの交点のx座標は
そして、この図形は点(π,0)に関して対称。
したがって、求める面積は
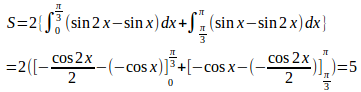
(解答終了)
問題2 次の図形の面積を求めよ。
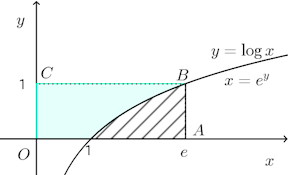
(1) 曲線y=logxとx軸、y軸および直線y=1で囲まれた部分。(2) 曲線と直線y=xとで囲まれた部分。
よって、求める面積Sは
求める面積は、□OABCから斜線部(x軸とy=logx、x=eで囲まれた部分)の面積を引いたものに等しいから
(2) 曲線と直線y=xとの交点のx座標は
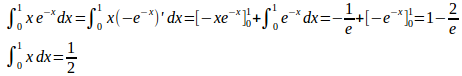
よって、
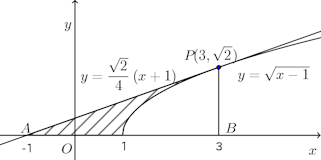
問題3 次の図形の面積を求めよ。
(1) 曲線と、点(3、√2)におけるこの曲線の接線およびx軸とで囲まれた部分
(2) 曲線y=logxと、この曲線の原点を通る接線およびx軸とで囲まれた部分
【解】
接点Pからx軸におろした垂線の足をBとすると、この図形の面積Sは
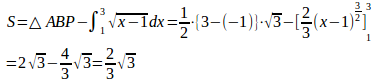
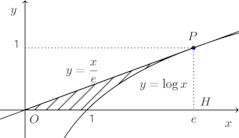 (2) 接点Pの座標を(t,logt)とすると、接線の方程式は
(2) 接点Pの座標を(t,logt)とすると、接線の方程式は
この問題3の(2)は、(1)同様に
問題4 y=ax²のグラフがy=logxのグラフと接するように定数aの値を定めよ。また、そのとき、これらのグラフとx軸とで囲まれる図形の面積を求めよ。
【解】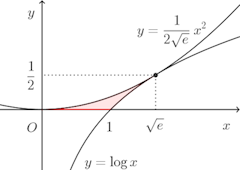 y=f(x)=ax²とy=g(x)=logxとの接点のx座標をtとすると、f(t)=g(t)、f'(t)=g'(t)。
y=f(x)=ax²とy=g(x)=logxとの接点のx座標をtとすると、f(t)=g(t)、f'(t)=g'(t)。
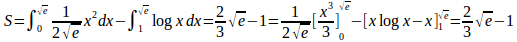
(解答終わり)