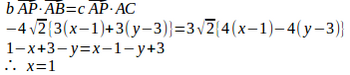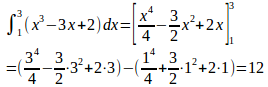定積分の問題2 [ネコ騙し数学]
定積分の問題2
問題1
【解】
極限の定義に従って計算すれば上のようになるけれど、g(t)=t²+atとおき、さらに
そして、
つまり、
このことを踏まえて次の問題!!
問題2 とするとき、次の極限値を求めよ。
よって、
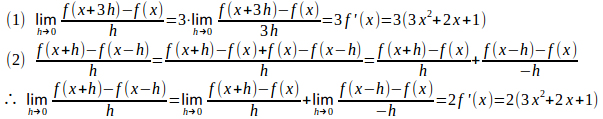
問題3 区間a≦x≦bにおいて、f'(x)>0を満たす関数f(x)に対して
【解】
区間a≦x≦bにおいて、f'(x)>0だから、f(xは、a≦x≦bにおいて(単調)増加。
したがって、
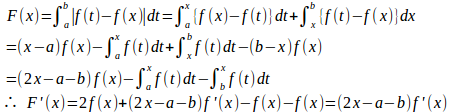
a≦x≦bでf'(x)>0だから、
となり、のときに極小、かつ、最小。
「定積分の問題」の回で取り上げた問題2、
問題2 a>0のとき、
や類題1は
類題1 実数aに対して
は、今回取り上げた問題の特殊なものであった。
ロピタルの定理 [ネコ騙し数学]
ロピタルの定理
平均値の定理には、コーシーの平均値と呼ばる次のものがある。
コーシーの平均値の定理
f(x)、g(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能、さらにg'(x)=0ならば
【証明】
h(x)は、[a,b]で連続、(a,b)で微分可能、かつ、h(a)=h(b)=0。
ロールの定理より
g'(x)はa<x<bでg'(x)≠0だから、g'(c)≠0。
よって、
(証明終わり)
この平均値の定理を使うと、次のロピタルの定理を証明することができる。
ロピタルの定理
f(a)=0、g(a)=0で、f(x)、g(x)がx=aを含む近傍で連続、x=a以外で微分可能とする。
x=aの近傍で、aとは異なる任意の数をxとすると、コーシーの平均値の定理より
仮定より、f(a)=0、g(a)=0だから
したがって、
(略証終わり)
感覚に訴えるかける証明で厳密なものではないけれど、ひとまず、これで納得していただけるのではないか。
このロピタルの定理は、0/0や∞/∞といった不定形の極限値を求める時に便利な定理である。
問題1 f(x)が連続な導関数をもつとき、次の極限を求めよ。
この問題では、x=aのとき、分子・分母ともに0で、0/0のタイプの不定形の極限。
ということで、ロピタルの定理が使える(かもしれない)。
問題2 次の極限を求めよ。
これは∞/∞の極限で、分子・分母ともに微分可能。
よって、ロピタルの定理より
(解答終わり?)
しかし、これはロピタルの定理の誤用。
−1≦cosx≦1だから、x−1≦x−cosx≦x+1。
また、次のような誤用もある。
問題3 次の極限を求めよ。
ロピタルの定理より
(解答終わり)
上の【解?】のどこがいけないかというと、
x=0のとき、cosx≠0で、そもそも、ロピタルの定理の前提条件を満たしていない!!そして、この極限は
このロピタルの定理は、この定理の理解不足による誤用が多いことで有名。
だから、この定理は極力使用は避けるべきで、極限を求める方法がどうしてもわからないときにのみ使用を限るべきだ。ベクトル 直線の方程式2の続き [ネコ騙し数学]
ベクトル 直線の方程式2の続き
問題1 直線lの方程式をax+by+c=0とする。
(1) lはベクトルと平行であることを示せ。
(2) P(x,y)、Q(x,y)からlにおろした垂線の足をそれぞれR、Sとするとき、RSの長さを求めよ。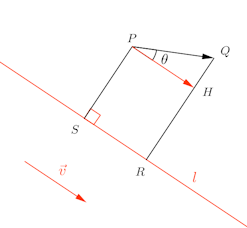
【解】
(1) 直線lはと垂直。
よって、と直線lは平行である。
(2) QからPRに垂線をおろし、垂線の足をHとし、QPとQHのなす角度をθとする。
問題2 △ABCと点Oがある。
(1) AからBCに引いた垂線上の点をPとし、とすると、
(2) 上の(1)を使って、△ABCの3垂線が1点で交わることを証明せよ。
【解】(1) AP⊥BCだから
(2) AからBCにおろした垂線とBからCAにおろした垂線の交点をPとする。
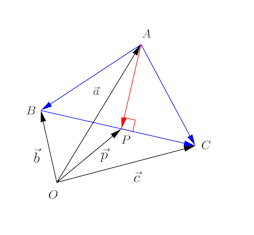
(1)より
(解答終わり)
問題3 △ABCにおいて、辺の長さをBC=a、CA=b、AB=cとする。
(1) △ABCの平面上の点Pが∠BACの2等分線(延長線も含む)の上にある条件は
(2) 3頂点の座標がA(1,3)、B(−2,0)、C(5,-1)のとき、∠BAC、∠ABCの2等分線の方程式を求めよ。また、△ABCの内心を求めよ。
【解】(1) ∠BAP=∠CAPだから
(2) ∠BACの2等分線上の点Pの座標を(x,y)とする。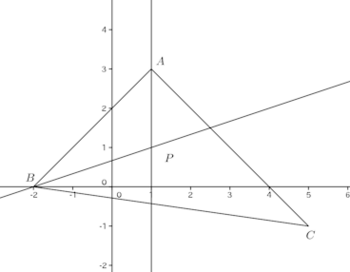
∠ABCの2等分線上の点Pの座標を(x,y)とすると、(1)より
である。
内心はx=1とx−3y+2=0の交点だから、内心は(1,1)である。
(解答終わり)内心Pを求めるだけならば、
という公式があるので、これを使ってもよい。
【公式の略証】与式の両辺をを引く。
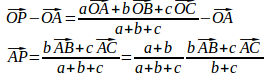
よって、点Pは、Aと辺ACをAB:ACに内分する点とを結ぶ直線、つまり、∠Aの2等分線上に存在する。
同様に、点Pは∠Bの2等分線上にあるので、点Pは△ABCの内心である。(略称終わり)
ベクトル 直線の方程式2(平面の場合) [ネコ騙し数学]
ベクトル 直線の方程式2(平面の場合)
平面上に、ベクトルに垂直で、位置ベクトル
の点P₀を通る直線lがあるとする。
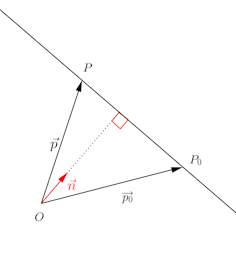
であり、
とすると、
は定数なので、
とおくと、上式は
さらに、とすると、次のようになる。
以上のことから、ax+by=cはに垂直な直線である。
問題1 原点Oから直線lへひいた垂線OHとx軸のなす角がαで、OHの長さがpのとき、lの方程式は
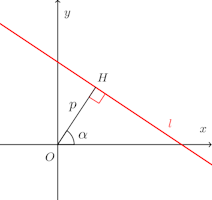
【解】
l上の動点をP(x,y)とする。条件より
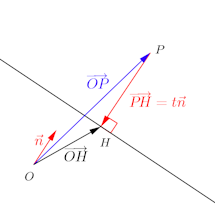
問題2 点P(x₀,y₀)から直線l:ax+by+c=0におろした垂線の足をHとするとき、推薦の長さPHを求めよ。
垂線PHは、ベクトルと平行。
自然な次の別解を。
【別解】
PHは、ベクトルと平行だから、
垂線の足Hをの座標を(x,y)とすると
そして、これで、直線l:ax+by+c=0と点P(x₀,y₀)の距離dの公式
定積分の問題 [ネコ騙し数学]
定積分の問題
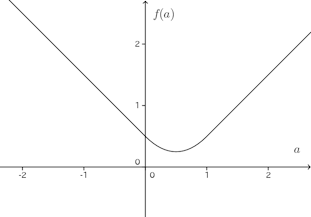
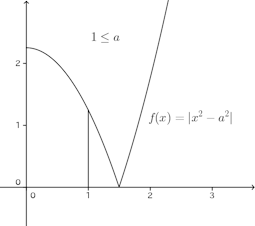
問題1 aの関数のグラフをかけ。
a≦0では、つねに|a−x|=x−a
0<a<1のとき、
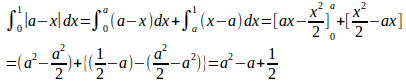
1≦aのでは、つねに|a−x|=a−x
よって
以上のことから、グラフは次のとおり。
(解答終わり)
問題2 a>0のとき、
【解】
0<a<1のとき
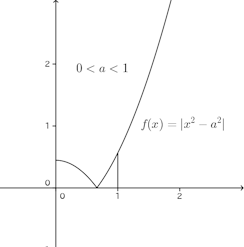
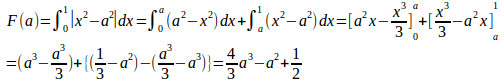
よって、
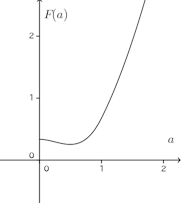
0<a<1でF(a)は微分可能で
したがって、0<a≦1ではa=1/2のとき最小。
1≦aのときF(a)は増加。以上のことより、a=1/2のとき、最小である。
(解答終わり)
類題1 実数aに対して
【答】
a=1/2のとき最小で、最小値7/32。問題1、問題2、類題1ともに、a=1/2!!
さらに、a>0とし、
これは偶然だろうか(^^)
問題3 次の等式を満たす関数f(x)を求めよ。
(1) は定数なので、
すると、
(2)
は定数なので
よって、
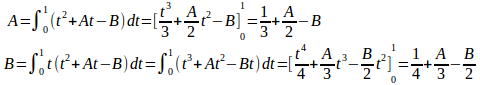
これを解くとA=3/13、B=17/78
よって、
ルジャンドルの多項式 [ネコ騙し数学]
ルジャンドルの多項式
問題1 任意の実数p,qに対して、次の成り立たせるような2次関数f(x)=x²+ax+bを求めよ。
【解】
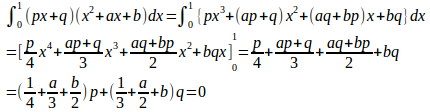
よって、
n−1次以下のすべての多項式Q(x)に関して
この一般形は
何故ならば、
ちなみに、
問題2 次の条件を満たすxの3次の整式P(x)を求めよ。
(ア) 任意の2次以下の整式Q(x)に対して
【解】
Q=ax²+bx+cであるとする。
P(x)=px³+qx²+rx+sとすると
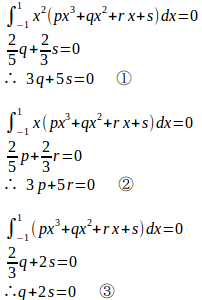
①、③よりq=s=0。
また、P(1)=1より
よって、
これは、次の公式を使えば出てくるが、
大学入試では、この公式は使えない!!ちなみに、この多項式をルジャンドル(Legendre)の多項式という。
上の定積分の計算では
これは公式というほどのものではなく、
ちなみに、
定積分の計算法 [ネコ騙し数学]
定積分の計算法
§1 定積分の計算法
F(x)をf(x)の原始関数、すなわち、
このとき、定積分(の計算法)は
ちなみに、∫の下についている添字のaを積分の下端、上についているbを積分の上端という。
例
定積分には、不定積分と同様に、以下の性質がある。
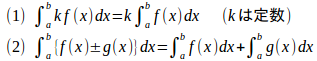
【略証】
F(x)、G(x)をf(x)、g(x)の原始関数とする。 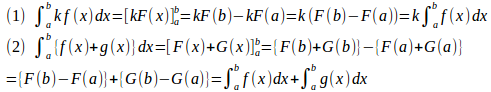
さらに、定積分には次のような性質がある。
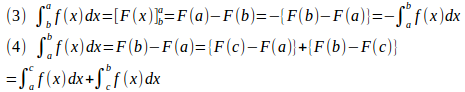
【略証終わり】
また、定積分の定義から明らかなように、
問題1 次の定積分の値を求めよ。
(解答終わり)
問題2 次のことを示せ。
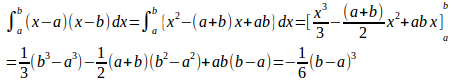
(解答終わり)
問題2の結果は公式のようなもの。これを知っていると、次の定積分は暗算で計算できる。
問題3 次の値を求めよ。
x²+x−2=(x+2)(x-1)
0≦x≦1でx²+x−2≦0、1≦x≦2ではx²+x−2≧0したがって、
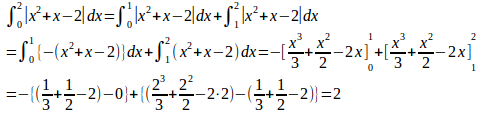
(解答終わり)
§2 微分と定積分の関係
xを変数とすると、
f(x)の原始関数をφ(x)とすれば、
問題4 (1)を計算し、(2)のf(x)を求めよ。
(1)
(2) 両辺を微分すると
不定積分の問題 [ネコ騙し数学]
不定積分の問題
問題1 xの関数について次のことが成り立つものとする。
ただし、を満足するとする。
(2) f(x)を求めよ。
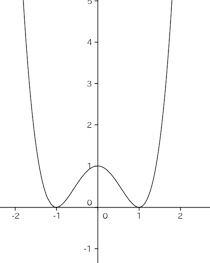
(3) f(x)の極値を求めて、グラフの概形をかけ。【解】
(1)
(2)
よって、
(3) f'(x)=4(x³−x)=4x(x+1)(x−1)
増減表はx | … | −1 | … | 0 | … | 1 | … |
f'(x) | − | 0 | + | 0 | − | 0 | + |
f(x) | 減少 | 0 | 増加 | 1 | 減少 | 0 | 増加 |
問題2 関数f(x)、g(x)が、任意の実数s、tに対して、常に
【解(?)】
s=0を代入すると
以上のことより、
f(x)=ax+b、g(x)=a(解答終わり)
しかし、これでは、微分積分を使っていない。
だから、微分を使って、こう解くべきなのだろう。【解】
s=0を代入すると
f(x)=ax+b、g(x)=a
(解答終わり)しかし、これでは不定積分を使っていない。
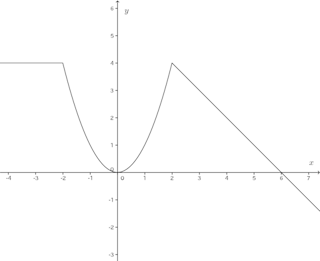
何故、この問題が不定積分の問題に紛れ込んでいるのだろう(・・?問題3 関数f(x)の導関数f'(x)が次のように与えられている。
【解】
x≦−2ではf'(x)=0
よって、①よりC₁=4。
②より
この図から明らかなように、x=0のときf(x)は極小で極小値は0。また、x=2のとき極大で極大値は4。
x=−2のところは、極大値の定義次第で、広義の極大であるけれど、狭義の極大ではない。
微分の不等式への応用 [ネコ騙し数学]
微分の不等式への応用
問題1 次の不等式を証明せよ。
(1) x>1のとき
(1) 左辺と右辺の差をとり
f(x)はx>1で微分可能。
したがって、x>1で
(2) 左辺と右辺の差をとり
f(x)はx>0で微分可能。
したがって、
問題2 a、b、cが正の数であるとき、
a³=α、b³=β、c³=γ(α>0、β>0、γ>0)とすると、上の式は次のように書き換えることができる。
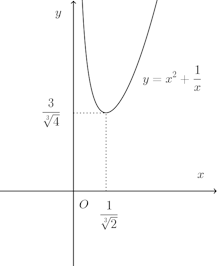
相加平均≧相乗平均を使って最小値を求めるとき、等号を満たすxが存在することを確かめないといけない。
等号が成立するxが存在しない場合もあるのでこの確認は絶対しなければならない。この程度ならば、微分したほうが楽。
上の問題では、f(x)の定義域をx>0としているけれど、
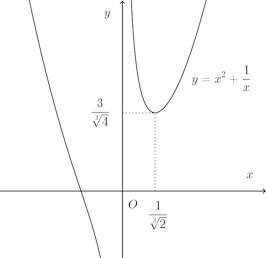
この図から明らかなように、極小値は存在するけれど、最小値は存在しない。
また、y=aとy=f(x)との交点を調べることにより、3次方程式
何故ならば、
この結果を使うと、
a>□のとき実数解は3つ、a=□のとき実数解は2つ、a<□のとき実数解は1つと判別することができる。ちなみに、1/xの微分は導関数のところで求めてある。
微分の方程式への応用 [ネコ騙し数学]
微分の方程式への応用
問題1 次の方程式の実数解の個数はどのようになっているか。
(1) x³−3x+1=0(2) x³−12x−a=0
【解】(1)
x | −∞ | … | −1 | … | 1 | … | +∞ |
f'(x) |
| + | 0 | − | 0 | + |
|
f(x) | −∞ | 増加 | 3 | 減少 | −1 | 増加 | +∞ |
グラフは次のとおり。
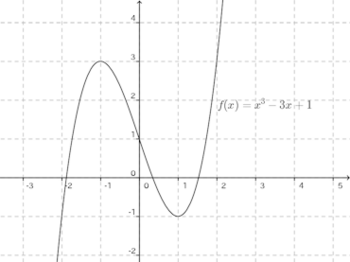
よって、実数解は3個。
x³−3x+1=0のα<β<γとする。
中間値の定理より、α、β、γは−2<α<−1、−1<β<1、1<γ<2に存在する。
(2)
x³−12x−a=0は、連立方程式y=x³−12xとy=aと同値。y=x³−12xの増減を調べる。
x | −∞ | … | −2 | … | 2 | … | +∞ |
y' |
| + | 0 | − | 0 | + |
|
y | −∞ | 増加 | 16 | 減少 | −16 | 増加 | +∞ |
y=x³−12xとy=aとの交点の数を調べる。
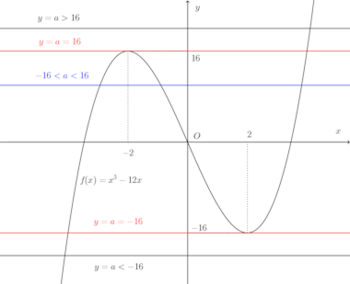
グラフより、
a>16のとき 1
a=16のとき 2−16<a<16のとき 3
a=−16のとき 2a<−16のとき 1
よって、実数解の個数は
a>16のとき 1
a=16のとき 2−16<a<16のとき 3
a=−16のとき 2a<−16のとき 1
である。(解答終わり)
問題2 次の方程式が異なる3つの実数解をもつようにaの値を定めよ。
よって、a>0でなければならない。
f(x)の増減表は
x | −∞ | … | −√a | … | √a | … | +∞ |
f'(x) |
| + | 0 | − | 0 | + |
|
f(x) | −∞ | 増加 | 2a√a+1 | 減少 | −2a√a+1 | 増加 | ∞ |
f(x)=0が実数解を3個もつためには、
問題4
(1) y=f(x)の増減を調べて、方程式f(x)=0は1つの実根をもつことを証明せよ。
(2) 方程式g(x)=0は実根を持たないことを証明せよ。【解】
(1)
f(−2)<0、f(−1)>0だから、f(x)=0の解は−2<x<−1にただ1つ存在する。
(2)
よって、g(x)は、x=αで極小値(最小値)をとる。
(解答終わり)
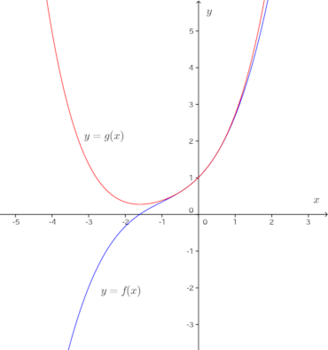
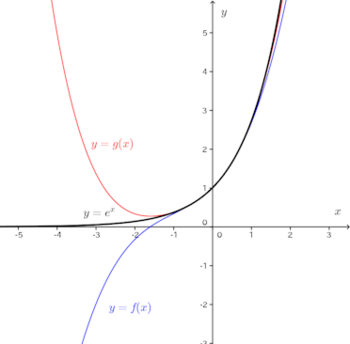
このグラフを見ると、−1≦x≦1で、f(x)とg(x)の値がよく一致していることが分かる。
ところで、マクローリン展開のところで
だから、この問題に出てくるf(x)やg(x)は、指数関数のべき乗展開の近似式と考えることができる。
このグラフに指数関数の曲線を加えると、次のようになる。