関数の最大・最小の応用問題 [ネコ騙し数学]
関数の最大・最小の応用問題
問題1 1辺の長さ4cmの正方形の厚紙の4隅から正方形を切り取って箱を作るのに、その容積をできるだけ大きくするには、1辺が何cmであればいいか。
【解】切り取る正方形の1辺をxcm(0<x<2)とすると、容積Vは
x | 0 | … | 2/3 | … | 2 |
V' |
| + | 0 | − |
|
V | 0 | 増加 | 128/27 | 減少 | 0 |
よって、容積が最大なのはx=2/3cmのとき。
問題2 曲線y=2x−x²のグラフと、x軸より上(y>0の部分)にあって、x軸に平行な直線との交点をP、Qとする。OP、OQ(Oは原点)を2辺とする平行4辺形の面積の最大値を求めよ。
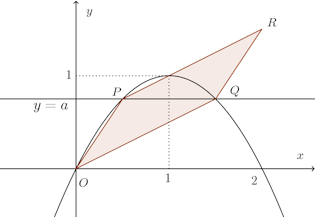
【解】
x軸に平行な直線y=a(0<a<1)と曲線y=2x−x²との交点のx座標を求める。
a | 0 | … | 2/3 | … | 1 |
f'(a) |
| + | 0 | − |
|
f(a) | (0) | 増加 | 4/27 | 減少 | (0) |
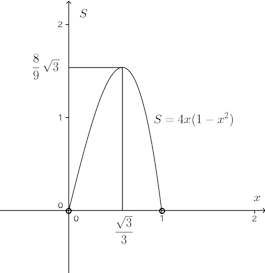
よって、a=2/3のときf(t)は最大でf(2/3)=4/27が最大値。
したがって、Sは、a=2/3のとき最大で、最大値は
(解答終わり)
問題3 直径ABの半円がある。この半円に図のように台形ABQPを内接させるとき、その台形の面積の最大値を求めよ。AB=2rとする。
【解】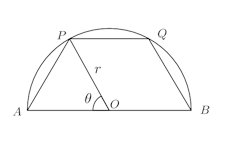
半円の中心をOとする。
台形の高さはrsinθ、PQ=2rcosθ。よって、台形の面積Sは
cosθ=xとすると、0<x<1だから
よって、x=1/2(θ=60°)のときに最大で、最大値は
(解答終了)
問題4 半径1の定円Oの周上に1点Aが与えられている。Aを中心とする円が、直径Oの直径AA'と交わる点をR、円Oと交わるを点P、Qとするとき、四角形APRQの面積の最大値を求めよ。
【解】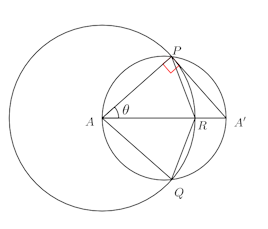
∠A'AP=θ(0°<θ<90°)とする。
PはAA'を直径ととする円周上の点なので∠APA'=∠R。よって、
(解答終わり)
関数の最大、最小 [ネコ騙し数学]
関数の最大、最小
問題1 xが−1から2まで変わる間に、関数2x³−x²−4xのとる値のうち、最大のものと最小のものを求めよ。
【解】y=2x³−x²−4xとすると、
x | −1 | … | −2/3 | … | 1 | … | 2 |
y' |
| + | 0 | − | 0 | + |
|
y | 1 | 増加 | 44/27(極大) | 減少 | −3(極小) | 増加 | 4 |
x=−2/3のとき最大で最大値は44/27、x=2のとき最小で最小値は−3。
(解答終わり)
この問題の場合、極大値は最大値になっていないことに注意。
関数の極大、極小は、あくまで、局所的な最大・最小にすぎない。また、問題1の場合、定義域は閉区間[−1,2](−1≦x≦2)、関数2x³−x²−4xは連続だから、関数の最大値、最小値は必ず存在するけれど、定義域を−1<x<2、つまり、(−1,2)とすると、最小値は−3で存在するが、最大値は存在しない。
問題2 閉区間[−1,4]における関数
【解】
|x|は、x≧0のときx、x<0のとき−x。よって、関数f(x)は
x | −1 | … | 0 | … | 2 | … | 4 |
y' |
| − | 0 | − | 0 | + |
|
y | 4 | 減少 | 0 | 減少 | −14(極小) | 増加 | 16 |
したがって、グラフは次のようになる。
閉区間[−1,4]のとき
最大値16 (x=4) 最小値0 (x=0)閉区間(−1,4)のとき
最大値なし 最小値0 (x=0)(解答終わり)
問題2の関数はx=0で微分可能でf'(0)=0である。増減表を見るとわかるけれど、x=0の前後でf'(x)の符号が変わっていないので、点(0,0)は極値ではないことに注意。
グラフを見れば明らかだけれど、この関数は閉区間[−1,2]で減少している!!
問題3 次の関数の最大値と最小値を求めよ。
t=sinxとおくと、0°≦x≦180°で0≦t≦1になる。
また、cos²x+sin²x=1よりcos²x=1−sin²x=1−t²となる。これを
t | 0 | … | 1/2 | … | 1 |
g'(t) |
| − | 0 | + |
|
g(t) | 3 | 減少 | 11/4 | 増加 | 4 |
よって、g(t)の最大値はt=1のときでg(1)=4が最大値。
0°≦x≦180°でt=sinx=1に対応するxの値はx=90°。また、g(t)はt=1/2のとき最小で、最小値は11/4。t=sinx=1/2に対応するxは30°と150°。
以上のことより、f(t)は
x=90°のとき最大で最大値は4x=30°、150°のとき最小で、最小値は11/4
(解答終わり)
関数の増減と極値2 [ネコ騙し数学]
関数の増減と極値2
問題1 次の関数のグラフをかけ。
【解】
よって、|x|≧1のとき
この増減表を書くと
x | … | −1 |
| 1 | … | 2 | … |
f'(x) | + |
|
|
| − | 0 | + |
f(x) | 増加 | −1 |
| 1 |
| −1 | 増加 |
|x|<1のとき
増減表を書くと
x | −1 | … | 0 | … | 1 |
f'(x) |
| − | 0 | + |
|
f(x) | −1 | 減少 | −3 | 増加 | 1 |
よって、グラフは次のようになる。
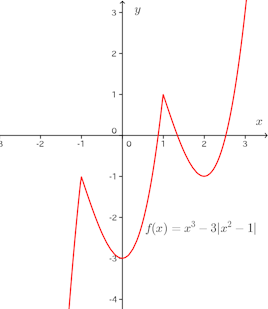
(解答終わり)
このグラフを見ると、f(x)がx=±1のところで局所的な最大である極大、x=0とx=2のところで局所的な最小である極小になっていることが分かると思う。
特にf(x)が極大になるx=±1のところに注目して欲しいのだけれど、ここは曲線が尖っていて微分可能ではない。つまり、f'(x)=0でなくても――そもそも微分係数が存在しない――、極値をとることがあるので注意が必要である。
ちなみに、
何故ならば、絶対値の中が非負、すなわち、x²−1≧0になるのは、x≦−1、x≧1のときであり、負になるのは−1<x<1のときだから。
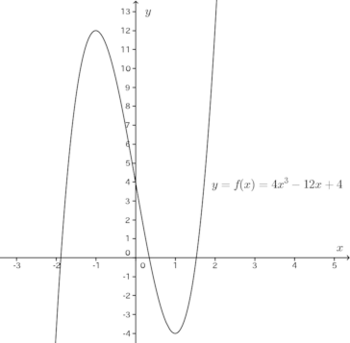
問題2 3次関数f(x)=4x³−3ax+bが極大値12と極小値−4をもつようにa、bの値を定めよ。
【解】
x | … | … | … | ||
f'(x) | + | 0 | − | 0 | + |
f(x) | 増加 | 極大 | 減少 | 極小 | 増加 |
よって、
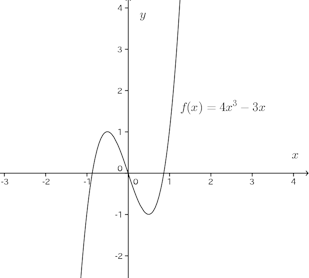
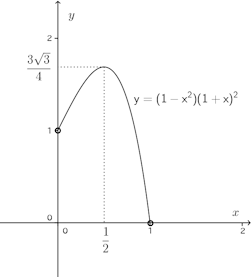
問題3 y=f(x)は3次関数で、そのグラフは原点に対して対称であり、x=1/2のときyは極小値−1をとる。y=f(x)を定め、yのグラフをかけ。
【解】
よって、f(x)=4x³−3x。
グラフは次の通り。この関数は原点対称なので、計算するまでもなく、x=1/2で極小値−1をとることから、x=−1/2で極大値1である。
問題に原点に対して対称とあるので、この関数は奇関数であり、
問題4
(1) y=x²(a−x)の極大値を求めよ。
【解】
(1) y'=2ax−3x²=x(2a−3x)これを0とする値は
a=0のとき、f(x)は単調減少で極大値はない。
a>0のとき、f(x)はx=2a/3で極大で、
(2) 極大値をM(a)とすると、グラフは次のようになる。
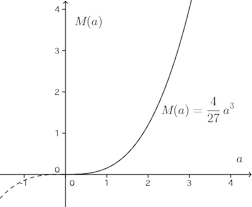
微分積分 関数の増減と極大・極小 [ネコ騙し数学]
微分積分 関数の増減と極大・極小
区間Iに属す任意の2数をx₁、x₂とする。
単調増加関数と単調減少関数をあわせて単調関数いう。
平均値の定理を再掲する。
平均値の定理
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能であるならば
さらに、次の定理。
定理
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能とする。開区間(a,b)でつねにf'(x)>0であれば、f(x)は開区間[a,b]で増加関数
開区間(a,b)でつねにf'(x)<0であれば、f(x)は開区間(a,b)で減少関数である。
【証明】開区間(a,b)でつねにf'(x)>0であれば、f(x)は開区間[a,b]で増加関数を証明する。
a≦x₁<x₂≦bとすれば、f(x)は[x₁,x₂]で連続、(x₁,x₂)で微分可能である。したがって、平均値の定理から
仮定よりf'(ξ)>0、x₂−x₁>0だから
開区間(a,b)でつねにf'(x)<0であれば、f(x)は開区間(a,b)で減少関数についても同様である。
(証明終わり)例
定義
x=aの近傍でf(a)がf(x)の最大値であるとき、関数f(x)はx=aにおいて極大であるといい、その値f(a)を極大値という。また、x=aの近傍でf(a)がf(x)の最小値であるとき、関数f(x)はx=aにおいて極小であるといい、その値f(a)を極小値という。
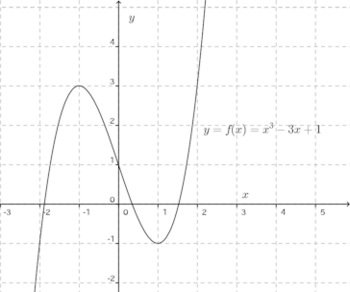
極大値、極小値をあわせて極値という。先に述べたf(x)=x³−3x+1の場合、x=−1の近傍、すなわち、δ>0が1に比べて十分小さいときx=−1の近傍、(−1−δ,−1+δ)でf(−1)=3が最大値なのでf(−1)=3はf(x)の極大値ということになる。同様に、x=1の近傍、(1−δ,1+δ)でf(1)=−1は最小値だからf(1)=−1はf(x)の極小値である。
また、この図から明らかなように、極大値は必ずしもf(x)の最大値にならないし、同様に極小値も必ずしもf(x)の最小値にならない。ちなみに、f(x)=x³−3x+1には最大値、最小値は存在しない。
定理(極値をとるための必要条件)
f(x)が区間Iで微分可能のとき、この区間のx₀でf(x)が極値をとるならば、f'(x₀)=0でなければならない。【証明】
f(x)がx=x₀で極大値をもつとき、x₁<x₀<x₂をみたす任意のx₁、x₂を区間内にとれば、f(x₁)<f(x₀)、f(x₀)>f(x₁)だから
極小のときも同様である。
(証明終わり)上の定理は、区間Iで微分可能な関数f(x)が極値をもつための必要条件であって、十分条件ではないこの注意する。
例 y=x³を微分するとy'=3x²。x=0でy'=0となるが、y=x³は単調増加関数で極値を持たない。
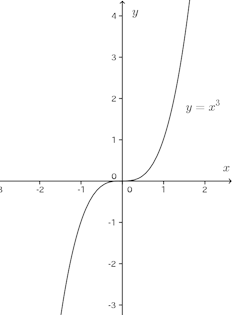
極値の判定法として次の定理をあげる。
定理
f'(a)=0かつx=aの前後でf'(x)が正から負に変われば、x=aで極大である。f'(a)=0かつx=aの前後でf'(x)が負から正に変わればx=aで極小である。
f'(a)=0かつx=aでf'(x)の符号が変わらなければ、f(a)は極値でない。上の定理を使うと、y=x³の場合、y=3x²で、x=0の前後のf'(x)の符号は+であり、符号が変わらないので、極値でないことが分かる。
問題1 次の問いに答えよ。
(1) 関数y=x³+3x²+12x−1はつねに増加関数であることを証明せよ。(2) 関数y=x³+ax²+12x−1が単調増加であるためのaの範囲を求めよ。
【解】(1)
(2) y'=3x²+2ax+12
これが単調増加であるためには、すべてのxについてy'≧0でなければならない。したがって、2次方程式3x²+2ax+12=0の判別式をDとすると、D≦0でなければならない。
問題2 次の関数の増減を調べ、グラフをかけ。
(1) y=x³−6x²+9x(2)
(1)
x | … | 1 | … | 3 | … |
y' | + | 0 | − | 0 | + |
y | 増加 | 4(極大) | 減少 | 0(極小) | 増加 |
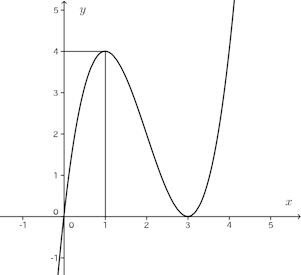
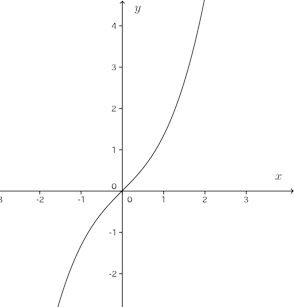
(2)
y'=3x²+1>0
微分積分 平均値の定理 [ネコ騙し数学]
微分積分 平均値の定理
この平均値の定理を証明するためには、次のロールの定理が必要である。
ロールの定理
f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能とする。f(a)=f(b)であるならば、
【証明】
f(x)は閉区間[a,b]で連続だから、[a,b]で最大値と最小値をとる。
f(x)が定数ならばf'(x)=0なので定理が成立。f(x)が定数でなければ、f(a)=f(b)とは異なる最小値または最大値のいずれかがaとbの間(a<c<b)に存在し、これをf(c)とする。
点cで微分可能だから
(証明終わり)
平均値の定理
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能であるならば
幾何的には、図のように、曲線上の2点A、Bを結ぶ線分ABに平行な接線がその2点で少なくとも1本ひけることを意味する。
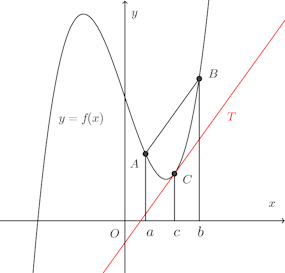
【証明】
g(x)は[a,b]っで連続、(a,b)で微分可能であり、g(a)=g(b)=0である。よって、ロールの定理より
したがって、
![]()
(証明終わり)
定理
f(x)、g(x)を区間Iで微分可能な関数とする。f'(x)がIでつねに0であるならば、f(x)は定数である。Iでつねにf'(x)=g'(x)ならば、f(x)−g(x)はIで定数である。【証明】
(前半の証明)a∈Iである点aを一つとる。
平均値の定理より、x∈Iの任意の点aに対して、aとxの間に
c∈Iだから条件よりf'(c)=0で、
(前半の証明終了)
(後半の証明)
h(x)=f(x)−g(x)とおくと、Iでh(x)は微分可能。Iでつねにf'(x)=g'(x)だから
よって、h(x)=f(x)−g(x)は定数である。
(後半の証明終わり)なぜ、この定理を紹介したかというと、不定積分の公式
導関数 [ネコ騙し数学]
導関数
§1 導関数の定義
区間Iで定義された関数f(x)がIの全ての点で微分可能であるとき、f(x)はIで微分可能であるという。また、このとき
y=f(x)の導関数を
xの増分、y=f(x)の増分をそれぞれΔx、Δyであらわす。つまり、
問 導関数の定義にもとづいて、つぎの導関数を求めよ。
(1) c (cは定数)(2) x+1
(3) x²(4)
【解】
(1) f(x)=c (定数)とすると
(2) f(x)=x+1とすると
よって、(x+1)'=1
(3) f(x)=x²とすると
(4) f(x)=1/xとすると
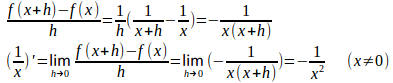
(5) f(x)=√xとすると、
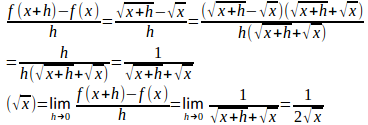
問題1 数学的帰納法を用いて、次のことを証明せよ。
nが正の定数のとき
【証明】
とする。
n=1のとき
n=kのとき、成り立つものとする。すなわち
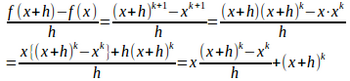
よって、
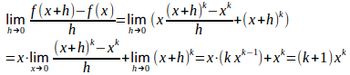
したがって、n+k+1のときにも成立する。
以上のことより、数学的帰納法によって
(証明終わり)
§2 導関数の公式
定義に従って、導関数を求めること、を微分することは面倒なので、実際に次の公式が使用される。
問 次の関数を微分せよ。
(1) y=3x+2(2) y=ax³−bx (a、bは定数)
【解】
問の(4)の結果
f(x)=g(x)=1/xとおくと、
となる。については、問題1と同様に数学的帰納法を使う。
【略証】
n=1のとき
で成立。
n=kのとき
n=k+1のとき
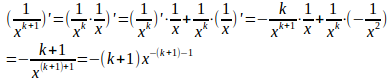
である。
(略証終わり)つまり、nが0以外の整数のとき、次の微分公式が成り立つことが証明された。
微分積分 曲線の接線の問題 [ネコ騙し数学]
微分積分 曲線の接線の問題
問題1 曲線y=x³の上の点Pにおける接線が、x軸、y軸と交わる点をそれぞれQ、Rとすれば、QはPRの3等分点であることを示せ。
【解】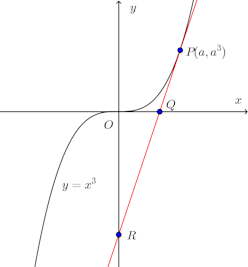
y'=3x²だから、P(a,a³)(a≠0)における接線の方程式は
よって、QはPRの3等分点である。
(解答終わり)
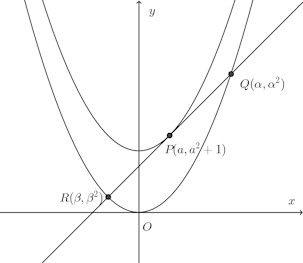
問題2 曲線y=x²+1上の任意の点Pにおける接線が曲線y=x²と交わる点をQ、Rとすると、PはQRの中点であることを証明せよ。
y'=2xだから、点P(a,a²+1)における接線の方程式は
また、2次方程式の解と係数の関係より
よって、PはQRの中点である。
(解答終わり)
問題3 曲線y=x²の直交する2つの接線の交点はどのような線上にあるか。
【解】y'=2xだからA(a,a²)における接線の方程式は
(解答終わり)
2次不等式と3次不等式の解について、ちょっと、ひとこと [ネコ騙し数学]
これから、微分法を用いて関数の増加減少を調べることになるけれど、
2次方程式くらいは解けるよな。
そして
2次不等式も解けるよな。
「2次不等式は解けません」ってんじゃ〜、話にならないぞ。
ということで、2次方程式と2次不等式の解き方を簡単に説明した過去の記事を紹介します。
ねこ騙し数学 番外編 二次方程式と二次関数
http://nekodamashi-math.blog.so-net.ne.jp/2015-04-07
わからない人はこの記事を読んでください。
2次不等式、2次不等式の基本は次のグラフ。
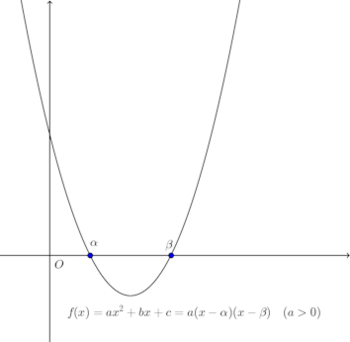
このグラフが頭の中に入っていれば、
ax²+bx+c=0 (a>0)
の相異なる2実根をα<βとするとき、
2次不等式
ax²+bx+c>0
の解がx<α,x>βであること、
ax²+bx+c<0
の解がα<x<βであることが分かる。
2次不等式に関しては覚えるのは、この図だけでいい!!
さらに3次方程式、ならびに、3次不等式の基本は次の図。
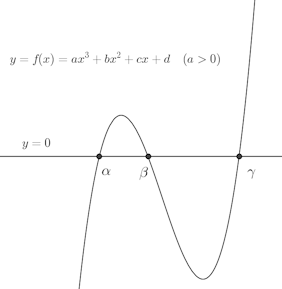
3次関数のこの図が頭の中に入っていれば、3次不等式、3次方程式で困ることはない。
f(x)=ax³+bx²+bx+c (a>0)
とし、f(x)=0の相異なる3実根をα、β、γ(α<β<γ)とすると、
f(x)>0になるのは、α<x<βとγ<x
f(x)<0になるのは、x<αとβ<x<γ
さらに、3次方程式f(x)=0が3つの実根を有する条件は、
極大値×極小値<0
であることが分かる。
接線の方程式 [ネコ騙し数学]
接線の方程式
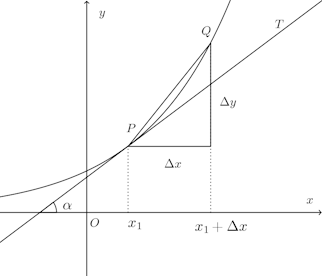
関数y=f(x)において、x=x₁、x=x₁+Δxに対応する点をP、Qとする。
このとき、平均変化率
Δx→0とすると、曲線上の点Qは限りなくPに近づき、平均変化率が一定の値に近づくならば、この一定値はx=x₁
における微分係数f'(x₁)であり、直線PQは点Pをとおり、傾きがf'(x₁)である直線PTに限りなく近づいてゆく。
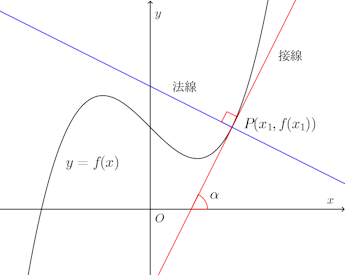
したがって、y=f(x)上の点P(x₁,f(x₁))における接線の方程式は、
また、接線とx軸がなす角をαとすると
点Pにおける法線の方程式は
上の式が点Pにおける法線を与えることは、接線と法線の方程式の傾きの積が−1であることより、明らかでしょう。
問題1 次の問いに答えよ。
(1) y=x³上の点(1,1)における接線と法線の方程式を求めよ。
(2) y=x³上の点(1,1)を通る接線の方程式を求めよ。
【解】(1) y'=3x²だから点(1,1)における接線の方程式は
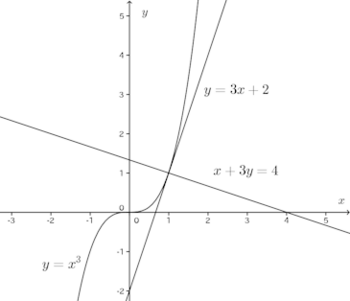
(2) 接点を(a,a²)とすると、接線の方程式は
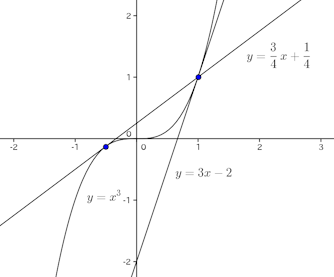
(解答終わり)
問題2 次の問いに答えよ。
(1) 曲線y=x³+ax²+bxが(−1,−5)において、y=2x−3に接するようにa、bの値を定めよ。(2) 曲線y=x³−ax+2が直線y=2xに接するようにaの値を定めよ。
【解】(1) y=f(x)=x³+ax²+bxとすると、
(2) y=f(x)=y=x³−ax+2
接点を(p,q)とすると、曲線y=x³−ax+2と直線y=2xは、この点を通るので
よって、
(解答終わり)
問題3 曲線y=ax³+4x+3は、係数aが変わっても
(1) すべて同一の点を通ることを示せ。(2) すべて同一の直線に接することを示せ。
【解】(1)
よって、x=0、y=3。
(2) y=f(x)=ax³+4x+3とすると
(解答終わり)
連続関数の性質 [ネコ騙し数学]
連続関数の性質
連続な関数には、次の性質がある。
定理1 f(x)、g(x)が区間Iで連続ならば、f(x)±g(x)、f(x)g(x)もIで連続である。また、g(x)≠0)ならば。f(x)/g(x)も連続である。
定理2 f(x)が区間Iで連続、g(x)が区間J(⊃f(I))で連続ならば、g(f(x))はIで連続である。
定理3 f(x)が点aで連続、かつ、f(a)≠0ならば、aの十分近くの点xでは、f(x)はf(a)と同符号である。
定理4 (中間値の定理) f(x)が閉区間[a,b]で連続、f(a)≠f(b)であるならば、f(a)とf(b)の間のすべての値γに対してf(c)=γを満たすcがa<c<bに存在する。
高校数学では、中間値の定理を次のように紹介していると思う。
定理4’ (中間値の定理) f(x)がa≦x≦bで連続な関数、f(a)とf(b)とが異符号ならば、f(c)=0になる点cがa<c<bに存在する。
【証明】f(a)<f(b)のとき、f(a)<γ<f(b)となる適当なγをとりg(x)=f(x)−γとすると、g(x)はa≦x≦bで連続な関数で、g(a)=f(a)−γ<0、g(b)=f(b)−γ>0となり、g(a)とg(b)は異符号。よって、定理4よりg(c)=0を満たすcがa<c<bに存在する。
f(a)>f(b)のとき、f(a)>γ>f(b)となる適当なγをとりg(x)=f(x)−γとすると、g(x)はa≦x≦bで連続な関数でg(a)=f(a)−γ>0、g(b)=f(b)−γ<0で異符号。
よって、定理4よりg(c)=0を満たすcがa<c<bに存在する。
逆に定理4’から定理4を証明することもできる。
例1 f(x)=xとし、−1≦x≦1とすると、f(−1)=−1、f(1)=1で異符号。また、f(x)=xは−1≦x≦1で連続なので、中間値の定理より、f(c)=0となるcが−1≦c≦1に存在する(c=0)。
例2 f(x)=x³−3xとし、−2≦x≦2とする。f(x)=x³−3xは−2≦x≦2で連続で、f(−2)=−2、f(2)=2と異符号。したがって、f(c)=0となるcが−2<c<2に存在する。
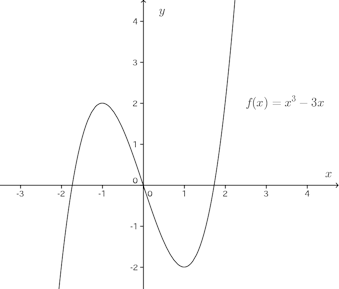
グラフから分かるように、この場合、f(c)=0となる点は一つではないことに注意(c=0、c=±√3)。
中間値の定理が保証する内容は、少なくとも一つf(c)=0となる点が存在していることを保証しているに過ぎない。
例3 f(x)=x²、−1≦x≦1のとき、f(±1)=1で同符号であるが、f(c)=0となる点cが−1<c<1に存在する(c=0)。したがって、中間値の定理を満たさなくても、a≦x≦bで連続な関数f(x)が、f(x)=0の解をもつことがある。
問 f(x)=1/xとすると、f(−1)=−1<0、f(1)=1>0であるが、−1<x<1でf(x)=0となる解を持たない。これは何故か、説明せよ。
【答】 x=0でf(x)=1/xは不連続だから。問題1 方程式ax²−x+1=0(aは実数)が実根をもつとき、1つの実根は2より大きくない正の数となることを証明せよ。
【解】(ⅰ) a=0のとき、x=1。
(ⅱ) a≠0のとき、ax²−x+1=0が実根をもつことより、この2次方程式の判別式をDとすると、
f(x)=ax²−x+1とすると、これは連続な関数で、
f(2)<0のとき、f(x)は連続な関数で、f(0)>0、f(2)<0だから、f(x)=0となる解が0<x<1に存在する。
(ⅰ)、(ⅱ)より、方程式ax²−x+1=0(aは実数)が実根をもつとき、1つの実根は2より大きくない正の数である。(解答終わり)
問題2 g(x)は0≦x≦1で連続な関数で、0≦g(x)≦1であるとき、g(c)=cとなる点cが存在することを証明せよ。
【解】(ⅰ) g(0)=0のとき、c=0とすればよい。(g(0)=0、g(1)=1の場合は、c=0、c=1のどちらでもよい)
(ⅱ) g(1)=1のとき、c=1とすればよい。(g(0)=0、g(1)=1の場合は、c=0、c=1のどちらでもよい)(ⅲ) 0<g(0)<1かつ0<g(1)<1の場合。
f(x)=g(x)−xとすると、f(x)は0≦x≦1で連続。さらに、
(ⅰ)、(ⅱ)、(ⅲ)より、
g(x)は0≦x≦1で連続な関数で、0≦g(x)≦1であるとき、g(c)=cとなる点cが存在する。
(解答終わり)最後に、連続関数の最大・最小値の定理を付け加える。
定理5 f(x)が閉区間[a,b]で連続のとき、f(x)は[a,b]で最大値、最小値をとる。
例4 f(x)=xとする。このとき、f(x)は連続な関数は−1<x<1で連続な関数であるが、−1<x<1でf(x)の最大値、最小値は存在しない。
また、のとき、−2<x<2と区間が開区間であっても、最大値、最小値が存在する。x=−1のとき、最大で最大値は2、x=1のとき最小で最小値は−2である。